Source Panel Method¶
Source Flow¶
Imagine a point source in 2D which all the streamlines are diverging fron the origin. Let the velocity components be $u_{r}$ in radial direction and $u_{\theta}=0$ in tangential direction. There are two important aspects of the source flow
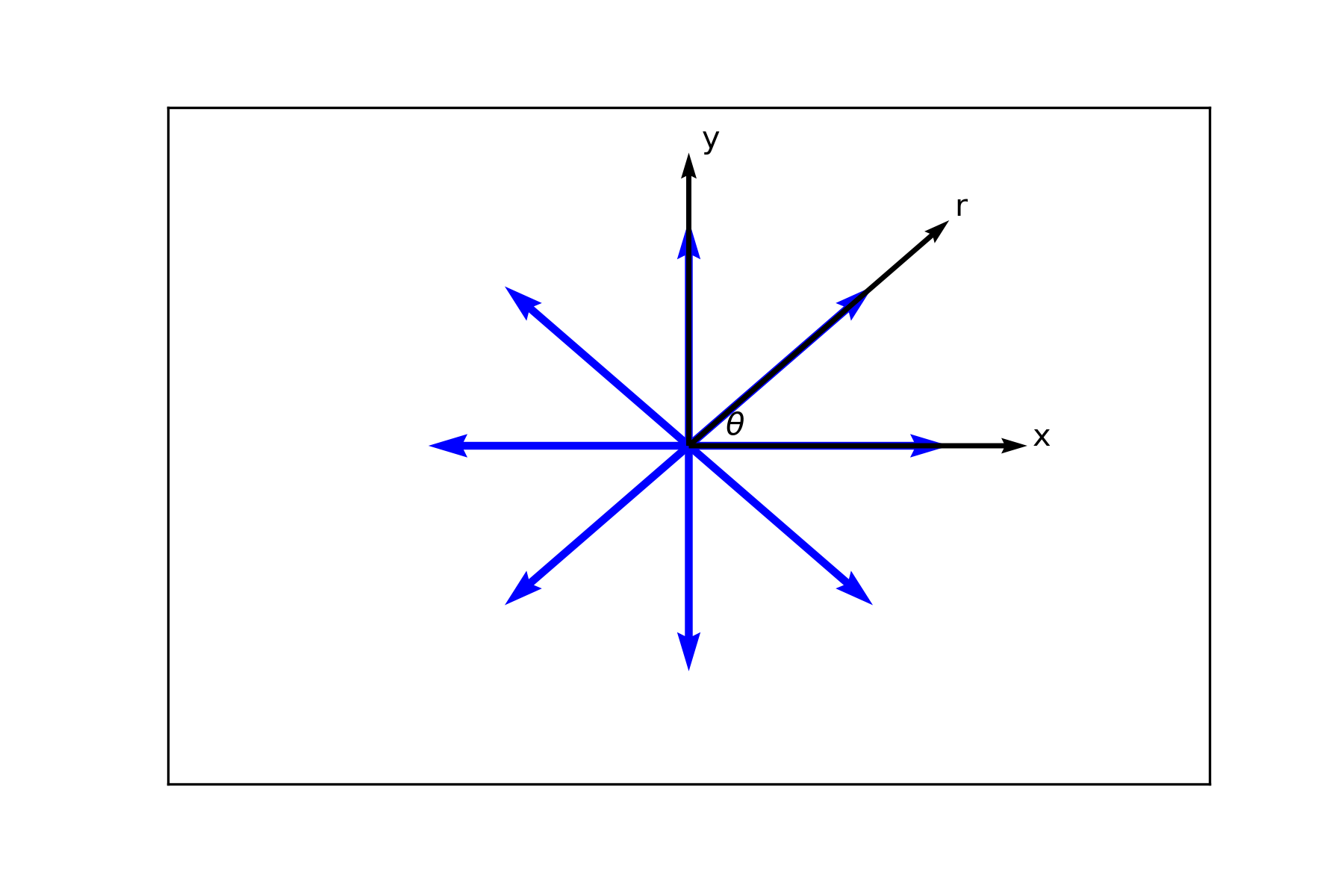
The flow is incompressible except at the origin $$\nabla\cdot \textbf{U}=\frac{1}{r}\frac{\partial}{\partial r}(ru_{r})+\frac{1}{r}\frac{\partial}{\partial \theta}u_{\theta}=0$$
The flow is irrotational everywhere $$\nabla\times \textbf{U}=\frac{1}{r}\frac{\partial}{\partial r}(ru_{\theta})-\frac{1}{r}\frac{\partial}{\partial \theta}u_{r}=0$$
Let $Q$ be the volume flow rate ($m^2/s$) at a distance $r$ from the origin, then
$$Q=2\pi ru_{r} \rightarrow u_{r}=\frac{Q}{2\pi r}$$
Here, $Q$ is called the "source strength". Now define the velocity potential $\phi$ as follows
$$u_{r}=\frac{\partial \phi}{\partial r}=\frac{Q}{2\pi r} \rightarrow \phi = \frac{Q}{2\pi}\ln r + f(\theta)$$
$$u_{\theta}=\frac{1}{r}\frac{\partial \phi}{\partial \theta}=0 \rightarrow \phi = c_{1}+f(r)$$
since the velocity potential is not a function of $\theta$ it can be defined in 2D as follows
$$ \phi = \frac{Q}{2\pi}\ln r$$
Source Panel Method¶
Consider an airfoil in a uniform flow field and place source points on the boundary of the airfoil. Let $q$ be the source strength per unit length.
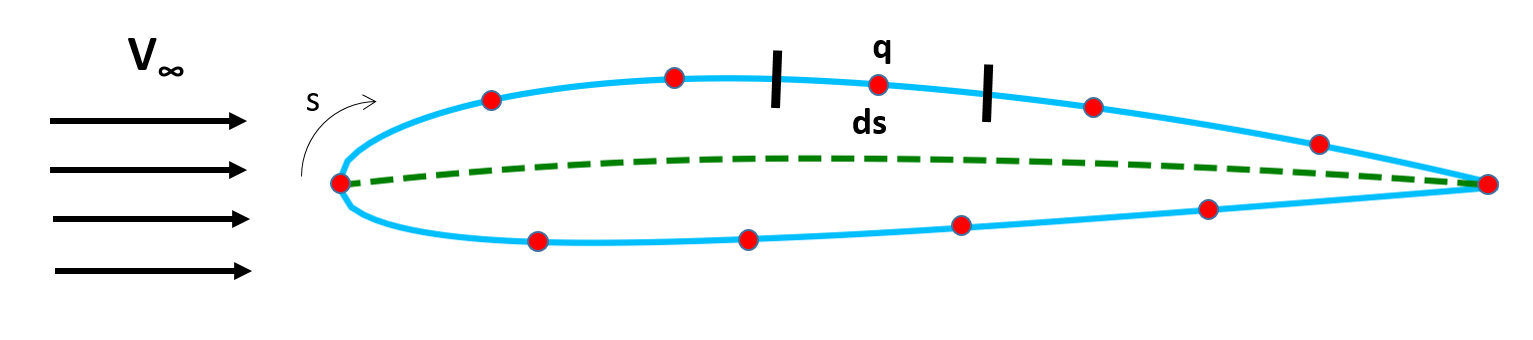The aim of this method is to find the discerete $q$ values which give the corresponding streamlines around the airfoil in combination with freestream $V_{\infty}$. After finding the potential around the airfoil, we can calculate the velocity and pressure distribution.
Let the potential induced by $qds$ at point P be $d\phi$
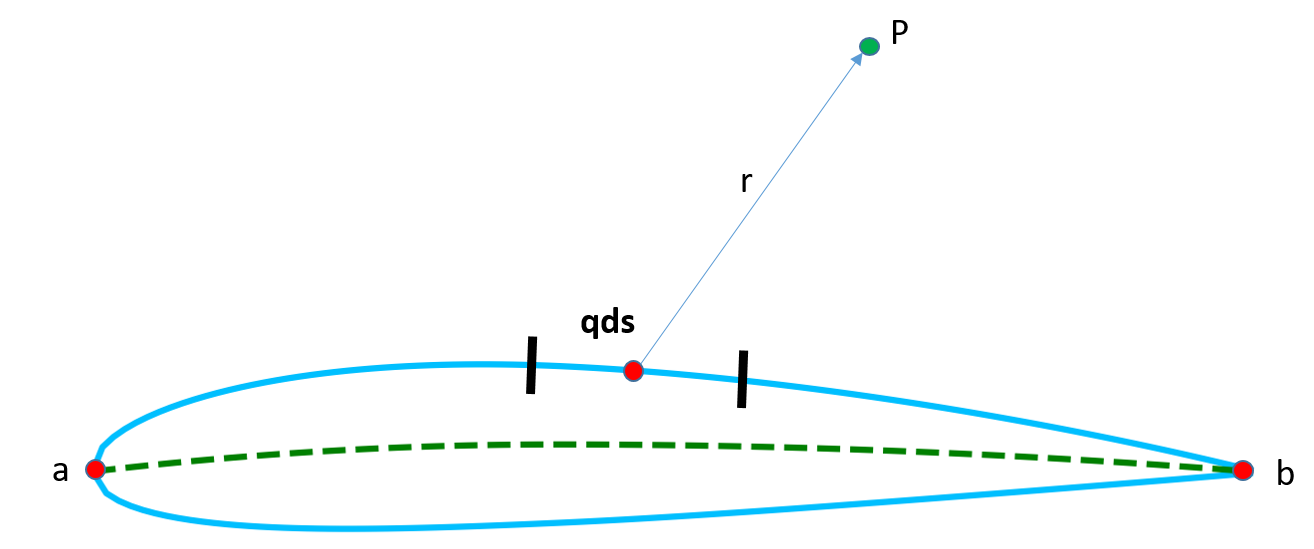
$$d\phi=\frac{qds}{2\pi}\ln r$$
then the total potential at P is
$$\phi=\int_{a}^{b}\frac{qds}{2\pi}\ln r$$
Let $q$ be constant over the given panel but varies from one panel to another. If we divide the surface to n panels then we have $q_{i}$ $i=1,2,...,n$. The problem is now to find each $q_{i}$.
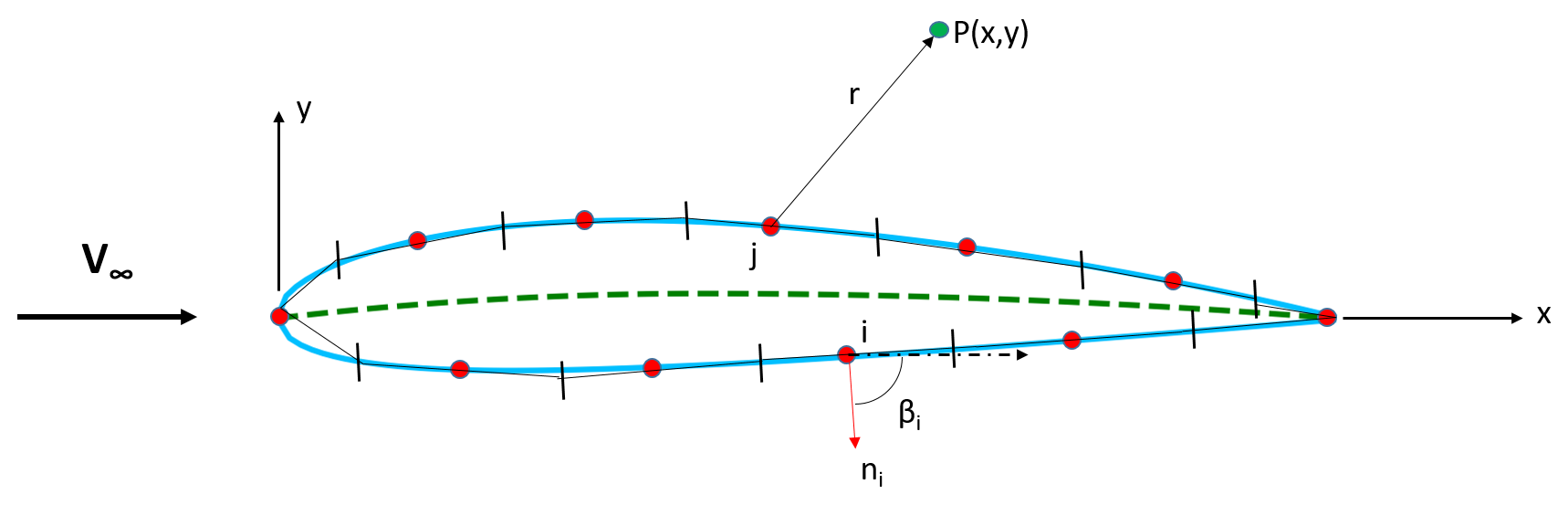The potential due to $j^{th}$ panel at point P is
$$\Delta \phi_{j}=\frac{q_{j}}{2\pi}\int_{j}\ln r_{pj}ds_{j}$$
Considering the contributions of all the panels
$$\phi(P)=\sum_{j=1}^{n}\Delta \phi_{j}=\sum_{j=1}^{n}\frac{q_{j}}{2\pi}\int_{j}\ln r_{pj}ds_{j}$$
where $r_{pj}=\sqrt{(x-x_{j})^{2}+(y-y_{j})^{2}}$. In order to find $\phi$ at the surface, we place point P at the $i^{th}$ panel
$$\phi(x_{i},y_{i})=\sum_{j=1}^{n}\frac{q_{j}}{2\pi}\int_{j}\ln r_{ij}ds_{j}$$
We need to impose boundary conditionson the panels where the normal component of the velocity is zero.
$$V_{\infty,n}=\textbf{V}_{\infty}\cdot \textbf{n}_{i}=V_{\infty}\cos \beta_{i}$$
$$V_{n}=\frac{\partial}{\partial n_{i}}\left[\phi(x_{i},y_{i})\right]=\frac{q_{i}}{2}+\sum_{\substack{j=1 \\ i\neq j}}^{n}\frac{q_{j}}{2\pi}\int_{j}\frac{\partial}{\partial n_{i}}(\ln r_{ij})ds_{j}$$
Therefore, the boundary condition for the surface velocity becomes
$$V_{\infty}\cos \beta_{i}+\frac{q_{i}}{2}+\sum_{\substack{j=1 \\ i\neq j}}^{n}\frac{q_{j}}{2\pi}\int_{j}\frac{\partial}{\partial n_{i}}(\ln r_{ij})ds_{j}=0 \tag{1}$$
This is the equation we need to solve in order to find $q_{i}'s$. This is a linear algebraic equation with n unknowns and n equations. After solving for $q_{i}'s$ the tangential velocity on the surface can be found as follows
$$V_{\infty,s}=V_{\infty}\sin \beta_{i}$$
$$V_{s}=\frac{\partial \phi}{\partial s}=\sum_{\substack{j=1 \\ i\neq j}}^{n}\frac{q_{j}}{2\pi}\int_{j}\frac{\partial}{\partial s}(\ln r_{ij})ds_{j}$$
Finally the velocity at each panel is
$$V_{i}=V_{\infty}\sin \beta_{i}+\sum_{\substack{j=1 \\ i\neq j}}^{n}\frac{q_{j}}{2\pi}\int_{j}\frac{\partial}{\partial s}(\ln r_{ij})ds_{j}$$
Then the pressure coefficient can be found as follows
$$c_{p,i}=1-\left[\frac{V_{i}}{V_{\infty}}\right]^{2}$$
In order to satisfy the mass conservation the following condition can be used
$$\sum_{j=1}^{n}q_{j}s_{j}=0$$
where $s_{j}$ is the lenght of the $j^{th}$ panel.
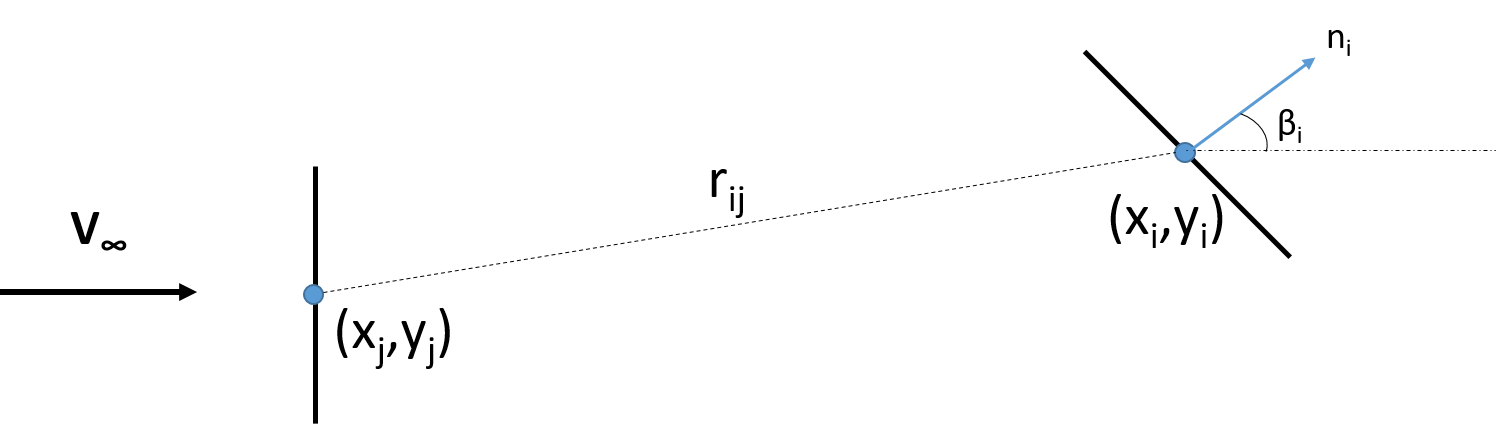
Now, let $I_{ij}$ be the integral in the equation (1), then in order to calculate $I_{ij}$, we use the chain rule
$$\frac{\partial}{\partial n}(\ln r)=\frac{\partial(\ln r)}{\partial r}\frac{\partial r}{\partial n}=\frac{1}{r}\frac{\partial r}{\partial n}$$
Again using the chain rule
$$\frac{\partial r}{\partial n}=\frac{\partial r}{\partial x}\frac{dx}{dn}+\frac{\partial y}{\partial y}\frac{dy}{dn}=\frac{1}{2}[r_{x}^{2}+r_{y}^{2}]^{-1/2}\left\{2r_{x}\frac{dx}{dn}+2r_{y}\frac{dy}{dn}
\right\}$$
where from the geometry
$$\frac{dx}{dn}=\cos \beta \hspace{5pt},\hspace{5pt}\frac{dy}{dn}=\sin \beta$$
Then the derivative becomes
$$\frac{\partial}{\partial n_{i}}(\ln r_{ij})=\frac{1}{r_{ij}}\frac{1}{2}\frac{1}{r_{ij}}\left[2r_{x}\cos\beta_{i}+2r_{y}\sin\beta_{i}\right]=\frac{1}{r_{ij}^{2}}\left[r_{x}\cos\beta_{i}+r_{y}\sin\beta_{i}\right]$$
In here, $(x_{i},y_{i})$ is the control point of the $i^{th}$ panel and $(X_{i},Y_{i})$, $X_{i+1},Y_{i+1}$ are boundary points, $n_{i}$ is the unit vector, $\beta_{i}$ is the direction of the unit vector and $\phi_{i}=\beta_{i}-\pi/2$, therefore
$$\sin \beta_{i}=\cos\phi_{i}$$
$$\cos\beta_{i}=-\sin\phi_{i}$$
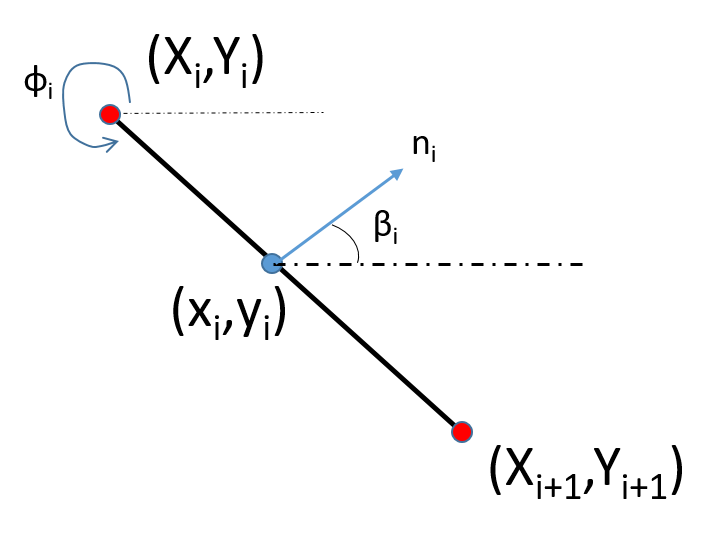Using the geometric relations we can write the following
$$x_{j}=X_{j}+s_{j}\cos\phi_{j}$$
$$y_{j}=Y_{j}+s_{j}\sin\phi_{j}$$
If we insert these relations into the derivation term in the integral we get
$$\frac{\partial}{\partial n_{i}}(\ln r_{ij})=\frac{-(x_{i}-X_{j}-s_{j}\cos\phi_{j})\sin\phi_{i}+(y_{i}-Y_{j}-s_{j}\sin\phi_{j})\cos\phi_{i}}{(x_{i}-X_{j}-s_{j}\cos\phi_{j})^{2}+(y_{i}-Y_{j}-s_{j}\sin\phi_{j})^{2}}$$
Rearranging terms using $\sin(A-B)=\sin A \cos B-\cos A \sin B$
$$\frac{\partial}{\partial n_{i}}(\ln r_{ij})=\frac{-x_{i}\sin\phi_{i}+X_{j}\sin\phi_{i}+s_{j}\cos\phi_{j}\sin\phi_{i}+y_{i}\cos\phi_{i}-Y_{j}\cos\phi_{i}-s_{j}\sin\phi_{j}\cos\phi_{i}}{x_{i}^{2}+X_{j}^{2}+s_{j}^{2}\cos^{2}\phi_{j}+y_{i}^{2}+Y_{j}^{2}+s_{j}^{2}\sin^{2}\phi_{j}-2x_{i}X_{j}-2x_{i}s_{j}\cos\phi_{j}+2X_{j}s_{j}\cos\phi_{j}-2y_{i}Y_{j}-2y_{i}s_{j}\sin\phi_{j}+2Y_{j}s_{j}\sin\phi_{j}}$$
Taking the relevant terms into paranthesis and using $\cos^{2}\phi_{j}+\sin^{2}\phi_{j}=1$ we get
$$\frac{\partial}{\partial n_{i}}(\ln r_{ij})=\frac{\sin(\phi_{i}-\phi_{j})s_{j}+(y_{i}-Y_{j})\cos\phi_{i}-(x_{i}-X_{j})\sin\phi_{i}}{(x_{i}-X_{j})^{2}+(y_{i}-Y_{j})^{2}+2s_{j}\left[-(x_{i}-X_{j})\cos\phi_{j}-(y_{i}-Y_{j})\sin\phi_{j}\right]+s_{j}^{2}}$$
If we let
$$A=-(x_{i}-X_{j})\cos\phi_{j}-(y_{i}-Y_{j})\sin\phi_{j}$$
$$B=(x_{i}-X_{j})^{2}+(y_{i}-Y_{j})^{2}$$
$$C=\sin(\phi_{i}-\phi_{j})$$
$$D=(y_{i}-Y_{j})\cos\phi_{i}-(x_{i}-X_{j})\sin\phi_{i}$$
finally the integral term in the equation (1) becomes
$$I_{ij}=\int_{0}^{s_{j}}\frac{Cs_{j}+D}{s_{j}^{2}+2As_{j}+B}ds_{j}$$
Using the integral tables we find
$$\int_{0}^{s_{j}}\frac{Cs+D}{s^{2}+2As+B}ds=\left[\frac{C}{2}\ln(s^{2}+2As+B)+\frac{D-AC}{\sqrt{B-A^{2}}}\arctan\left(\frac{s+A}{\sqrt{B-A^{2}}}\right) \right]_{0}^{s_{j}}$$
$$\int_{0}^{s_{j}}\frac{Cs+D}{s^{2}+2As+B}ds=\frac{C}{2}\ln(s_{j}^{2}+2As_{j}+B)+\frac{D-AC}{\sqrt{B-A^{2}}}\left[\arctan \left(\frac{s_{j}+A}{\sqrt{B-A^{2}}}\right) -\arctan \left(\frac{A}{\sqrt{B-A^{2}}}\right) \right]$$
This expression can be applied to any given shape. Once the integral is evaluated at each panel then they are insertes to the coefficient matrix [A]. The right hand side vector {b} is constructed from the known values from the boundary conditions and the linear system
is solved for unknown q's.
<< 3.1.2 NACA 5 Digit Series || Contents || 4.1.1 Example: Non-Lifting Flow Over a Circular Cylinder >>
References:
[1] Fundamentals of Aerodynamics, J.D. Anderson, McGraw-Hill Education, 2001.
[2] An Introduction to Theoretical and Computational Aerodynemocs, Jack Moran, Dover Publications, 2010.