NACA 5 Digit Airfoils:¶
NACA 5 digit series (LPQXX) are formulated as follows. The first digit L is the measure of the camber, when L is multiplied by (3/20) it gives the design lift coefficient ($C_{l}$). The second digit P determines the location of the maximum camber ($x_{mc}$) when multiplied by $0.05$ in tenths of $c$. The third digit (Q) specifies whether the airfoil has a standard camber (Q=0) or reflexed camber (Q=1). The reflexed cambered airfoils are designed to produce zero pitching moment. The last two digits ($XX$) give the maximum thickness of the airfoil in percentage of $c$. The camber line equation for 5 digit series depends on whether the airoil is reflexed or not. The equations for the standard series are as follows
$$y_{c}=\frac{c*k_{1}}{6}\left[\left(\frac{x}{c}\right)^3-3r\left(\frac{x}{c}\right)^2+r^2(3-r)\frac
{x}{c}\right] \hspace{10pt} \textrm{for }0\leq \frac{x}{c} \lt r $$
$$\frac{dy_{c}}{dx}=\frac{k_{1}}{6}\left[3\left(\frac{x}{c}\right)^2-6r\frac{x}{c}+r^2(3-r)\right] \hspace{10pt} \textrm{for }0\leq \frac{x}{c} \lt r $$
$$y_{c}=\frac{c*k_{1}r^3}{6}\left[1-\frac{x}{c}\right] \hspace{10pt} \textrm{for }r \leq \frac{x}{c} \leq 1$$
$$\frac{dy_{c}}{dx}=-\frac{k_{1}r^3}{6}\hspace{10pt} \textrm{for }r\leq \frac{x}{c} \lt 1 $$
The parameter (r) in above equations is related to maximum camber position ($x_{mc}$=0.05P) with the formula below and it is found by iteration for the given $x_mc$
$$x_{mc}=r\left[1-\sqrt{\frac{r}{3}}\right]$$
And $k_1$ is calculated to give prescribed lift coefficient ($C_li$) in combination with r, using the formula below
$$k_1 = \frac{6*(0.15L)}{N}$$
where N is a function of r
$$N=\frac{3r-7r^2+8r^3-4r^4}{\sqrt{r-r^2}}-\frac{3}{2}(1-2r)\left[\frac{\pi}{2}-arcsin(1-2r)\right]$$
The equations for the reflexed series
$$y_{c}=\frac{c*k_{1}}{6}\left[\left(\frac{x}{c}-r\right)^3-\frac{k_2}{k_1}(1-r)^3\frac{x}{c}-r^3\frac{x}{c}+r^3\right] \hspace{10pt} \textrm{for }0\leq \frac{x}{c} \lt r $$
$$\frac{dy_{c}}{dx}=\frac{k_{1}}{6}\left[3\left(\frac{x}{c}-r\right)^2-\frac{k_2}{k_1}(1-r)^3-r^3\right] \hspace{10pt} \textrm{for }0\leq \frac{x}{c} \lt r $$
$$y_{c}=\frac{c*k_{1}}{6}\left[\frac{k_2}{k_1}\left(\frac{x}{c}-r\right)^3-\frac{k_2}{k_1}(1-r)^3\frac{x}{c}-r^3\frac{x}{c}+r^3\right] \hspace{10pt} \textrm{for }r \leq \frac{x}{c} \leq 1$$
$$\frac{dy_{c}}{dx}=\frac{k_{1}}{6}\left[3\frac{k_2}{k_1}\left(\frac{x}{c}-r\right)^2-\frac{k_2}{k_1}(1-r)^3-r^3\right]\hspace{10pt} \textrm{for }r\leq \frac{x}{c} \lt 1 $$
The parameters r, $k_1$ and $k_2/k_1$ are computed ina different way then the standard series. First the r value is calculated for a given $x_{mc}$ that will make the pitching moment zero. Than the corresponding $k_1$ value that will make the prescribed lift coefficint $C_{li}=0.3$ is found. For the $k_2/k_1$ value the following formula is used
$$\frac{k_2}{k_1}=\frac{3(r-x_{mc})^2-r^3}{(1-r)^3}$$
The coefficients in the above equations are tabulated below for $C_{l}=0.3$
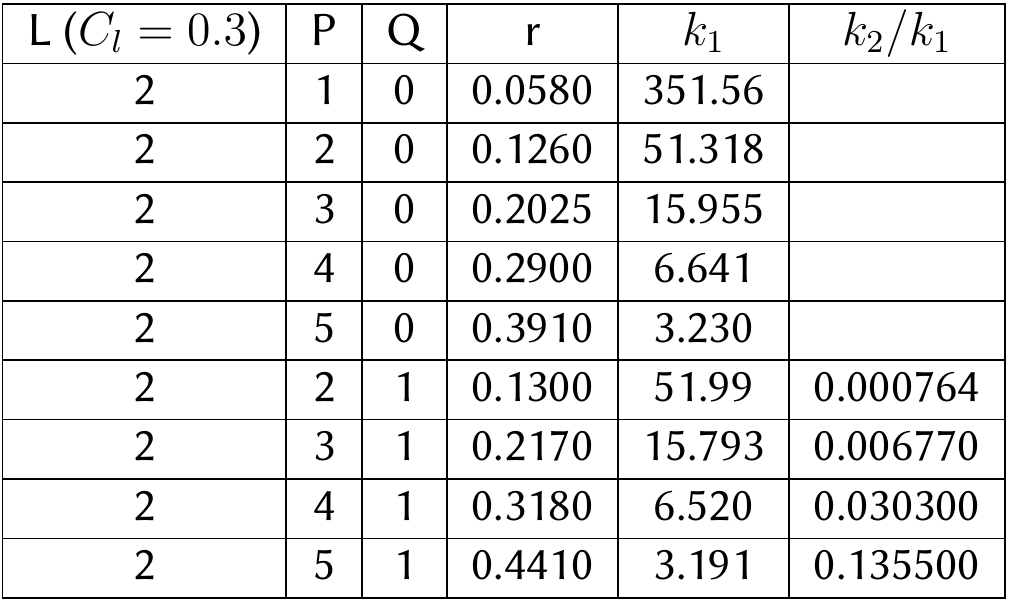
Thickness distribution and the surface coordinates are calculated using the steps as 4 digit series.
Here is an example python code for generating NACA 5 Digit airfoils.
import numpy as np
import matplotlib.pyplot as plot
import math as mt
# NACA 5 Digit Airfoil Generation
l = 2 # camber parameter
p = 3 # position of maximum camber parameter
q = 1 # standard or reflexed
t = 12 # maximum thichkness
c = 2 # chord length
t = 0.01*t
# Coefficients for 5 digit series
a0 = 1.4845
a1 = -0.6300
a2 = -1.7580
a3 = 1.4215
a4 = -0.5075
n = 100 # number of points along the chord
x = np.linspace(0,c,n) # x coordinate of points along the chord
y = np.zeros(n) # x coordinate of points along the chord
yc = np.zeros(n) # y coordinate of the camber line
dyc = np.zeros(n) # gradient of the camber line
yt = np.zeros(n) # thickness distribution
xu = np.zeros(n) # x coordinate of the upper surface
yu = np.zeros(n) # y coordinate of the upper surface
xl = np.zeros(n) # x coordinate of the lower surface
yl = np.zeros(n) # y coordinate of the lower surface
if q == 0: # standard series
xcm = 0.1*(p/2) # maximum camber position in tenths of chord
# Fixed point iteration for parameter r
r_old = 0.1 # initial guess for r
diff = 1 # difference bewtween r and r_old, assign any value to start while loop
tol = 0.0001 # tolerence
while diff > tol:
r = xcm + r_old*mt.sqrt(r_old/3)
diff = abs(r-r_old)
r_old = r
# Calculation of k_1
qm = (3*r-7*r**2+8*r**3-4*r**4)/(mt.sqrt(r-r**2))-(3/2)*(1-2*r)*((mt.pi/2)-mt.asin(1-2*r))
k1 = (6*(0.3*l/2))/qm
for i in range(n):
if (x[i]/c < r):
yc[i] = (c*k1/6)*((x[i]/c)**3-3*r*(x[i]/c)**2+r**2*(3-r)*(x[i]/c))
dyc[i] = (k1/6)*(3*(x[i]/c)**2-6*r*(x[i]/c)+r**2*(3-r))
else:
yc[i] = (c*k1/6)*r**3*(1-(x[i]/c))
dyc[i] = -(k1/6)*r**3
else: # reflexed series
xcm = 0.1*(p/2) # maximum camber position in tenths of chord
r = 0.2170 # r for 23112
k1 = 15.793 # k_1 for 23112
k21 = (3*(r-xcm)**2-r**3)/(1-r)**3 # k_2/k_1 for 23112
for i in range(n):
if (x[i]/c < r):
yc[i] = (c*k1/6)*(((x[i]/c)-r)**3-k21*(1-r)**3*(x[i]/c)-r**3*(x[i]/c)+r**3)
dyc[i] = (k1/6)*(3*((x[i]/c)-r)**2-k21*(1-r)**3-r**3)
else:
yc[i] = (c*k1/6)*(k21*((x[i]/c)-r)**3-k21*(1-r)**3*(x[i]/c)-r**3*(x[i]/c)+r**3)
dyc[i] = (k1/6)*(3*k21*((x[i]/c)-r)**2-k21*(1-r)**3-r**3)
for i in range(n):
yt[i] = (t*c)*(a0*mt.sqrt(x[i]/c)+a1*(x[i]/c)+a2*(x[i]/c)**2+a3*(x[i]/c)**3+a4*(x[i]/c)**4)
teta = mt.atan(dyc[i])
xu[i] = x[i] - yt[i]*mt.sin(teta)
xl[i] = x[i] + yt[i]*mt.sin(teta)
yu[i] = yc[i] + yt[i]*mt.cos(teta)
yl[i] = yc[i] - yt[i]*mt.cos(teta)
plot.xlim(-0.2,c+0.2)
plot.ylim(-c/3,c/3)
plot.plot(xu,yu,color='deepskyblue')
plot.plot(xl,yl,color='deepskyblue')
plot.plot(x,yc,'g--')
plot.yticks([])
plot.xticks([])
plot.show()
<< 3.1.1 NACA 4 Digit Airfoils || Contents || 4.1 Source Panel Method >>
References:
[1] Summary of Airfoil Data, I.H. Abbott, A.E. von Doenhoff, L.S. Stevers, Jr, NACA Report No. 824, 1945.
[2] www.airfoiltools.com