Substantial Derivative¶
Let $a=a(x,y,t)$ be any scalar or vector quantity of a fluid element in 2D. Assume the fluid element travels from point 1 to 2 and if $a_{1}$ is the value at $(x_{1},y_{1},t_{1})$, the value $a_{2}$ can be approximated by using Taylor series expansion
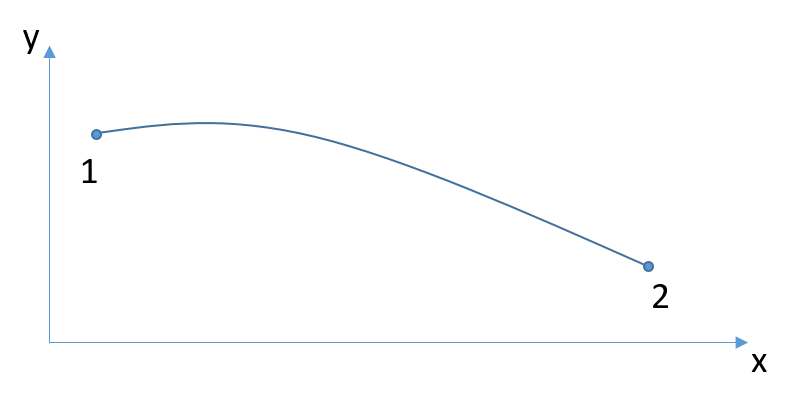
$$
a_{2}=a_{1}+\left(\frac{\partial a}{\partial t}\right)_{1}\Delta t+\left(\frac{\partial a}{\partial x}\right)_{1}\Delta x+\left(\frac{\partial a}{\partial y}\right)_{1}\Delta y+\left(\frac{\partial^{2} a}{\partial t^{2}}\right)_{1}\frac{\Delta t^{2}}{2}+\left(\frac{\partial^{2} a}{\partial x^{2}}\right)_{1}\frac{\Delta x^{2}}{2}+\left(\frac{\partial^{2} a}{\partial y^{2}}\right)_{1}\frac{\Delta y^{2}}{2}+\textrm{Higher Order Terms}
$$
If $\Delta x$, $\Delta y$ and $\Delta t$ are small enough higher order terms are neglegted and rearranging the above relation gives
$$\frac{a_{2}-a_{1}}{\Delta t}=\left(\frac{\partial a}{\partial t}\right)_{1}+\left(\frac{\partial a}{\partial x}\right)_{1}\frac{\Delta x}{\Delta t}+\left(\frac{\partial a}{\partial y}\right)_{1}\frac{\Delta y}{\Delta t}$$
In the limit that $\Delta t$ goes to zero
$$\lim\limits_{\Delta t \rightarrow 0}\frac{a_{2}-a_{1}}{\Delta t}=\frac{\partial a}{\partial t}+u\frac{\partial a}{\partial x}+v\frac{\partial a}{\partial y}=\frac{Da}{Dt}$$
This is called the substantial (or Material or Total) derivative of quantity a. The time derivative corresponds to local part and the remaining terms constitute the convective part due te velocity.
$$\frac{Da}{Dt}=\frac{\partial a}{\partial t}+(\textbf{U}\cdot\nabla)a$$
For a physical example of substantial derivative, imagine yourself holding a cup of tea and walking from your house to outside where the weather is very cold. As you walk outside the temperature of the tea will change due to your movement (change due to convection). Also, if you put an ice cube into the cup, the temperature will decrease with time because of ice whether you walk outside or not and this represents the local change in temperature. The combined effect of your movement and the ice is the substantial derivative of the temperature of the tea.
<< 1.2 Vector Differential Operator || Contents || 2.2 Conservation of Mass >>