DERIVATION OF MOMENTUM EQUATION¶
The derivation of the momentum equation is based on the following physical facts:
- Newton's second law: $m\textbf{a}=\textbf{F}$
two main sorces of force: surface and body forces
- surface forces: act on the surface of the element, pressure force and viscous forces
- body forces: act on the whole volume, gravitational forces, electromagnetic forces, Coriolis, etc.
There are several approaches to derive the momentum equation, the following approach is the fixed fluid element model described in [1]. Consider an infinitesimally small cubic fluid element with sides $\Delta x$, $\Delta y$ and $\Delta z$.
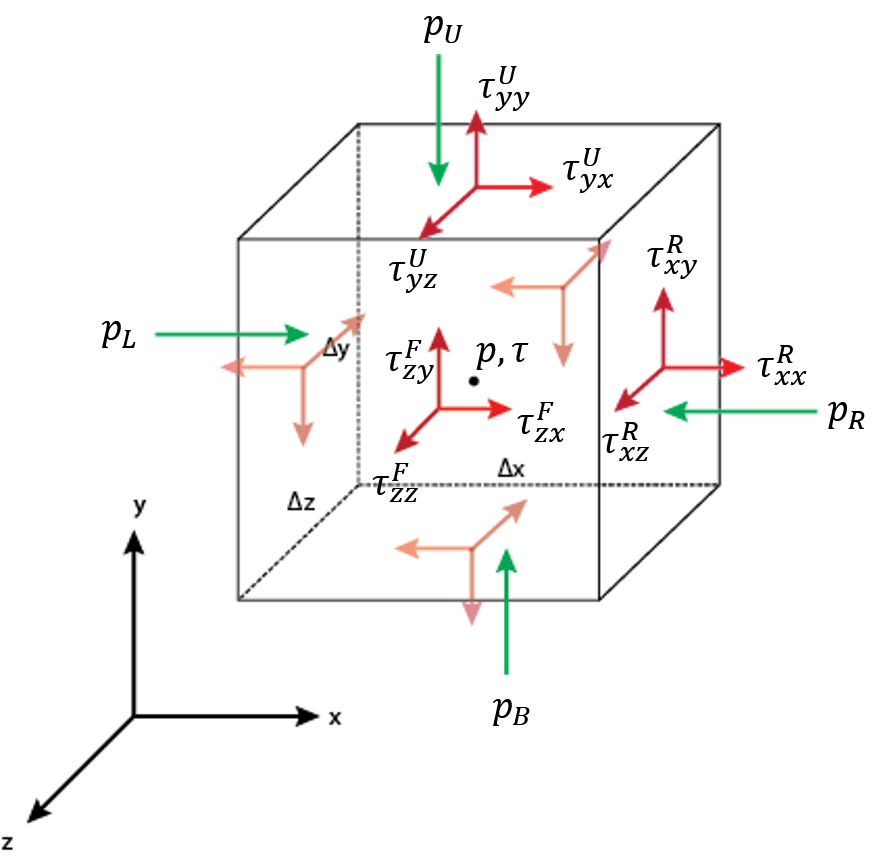
Body Forces:¶
Let $\textbf{f}$ be any body force per unit mass acting on the fluid element, then the body force is
$$\textbf{F}^{b}=\rho \textbf{f}\Delta x \Delta y \Delta z$$
Surface Forces:¶
The pressure and the shear stress at the centre of the element are $p$, $\tau$, respectively. The pressure and shear stress on the faces of the element can be calculated using Taylor series. Notice that the pressure force acts on the surface opposite to surface normal direction. Consider the forces on the right and left surfaces:
$$\textrm{on left face }p_{L}= \left[p-\frac{\partial p}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z \hspace{10pt},\hspace{10pt} \textrm{on right face }p_{R}=\left[p+\frac{\partial p}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z$$
$$\textrm{on left face }\tau_{xx}^{L}=\left[\tau_{xx}-\frac{\partial \tau_{xx}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z \hspace{10pt},\hspace{10pt} \textrm{on right face }\tau_{xx}^{R}=\left[\tau_{xx}+\frac{\partial \tau_{xx}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z$$
$$\textrm{on left face }\tau_{xy}^{L}=\left[\tau_{xy}-\frac{\partial \tau_{xy}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z \hspace{10pt},\hspace{10pt} \textrm{on right face }\tau_{xy}^{R}=\left[\tau_{xy}+\frac{\partial \tau_{xy}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z$$
$$\textrm{on left face }\tau_{xz}^{L}=\left[\tau_{xz}-\frac{\partial \tau_{xz}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z \hspace{10pt},\hspace{10pt} \textrm{on right face }\tau_{xz}^{R}=\left[\tau_{xz}+\frac{\partial \tau_{xz}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z$$
The remaining forces on the upper, bottom, front and back surfaces are written using the same formulation. Then net surface force along the $x-$ direction is as follows
$$F^{s}_{x}= \left[p-\frac{\partial p}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z -\left[p+\frac{\partial p}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z
+\left[\tau_{xx}+\frac{\partial \tau_{xx}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z-\left[\tau_{xx}-\frac{\partial \tau_{xx}}{\partial x}\frac{\Delta x}{2}\right]\Delta y \Delta z
+\left[\tau_{yx}+\frac{\partial \tau_{yx}}{\partial y}\frac{\Delta y}{2}\right]\Delta x \Delta z-\left[\tau_{yx}-\frac{\partial \tau_{yx}}{\partial y}\frac{\Delta y}{2}\right]\Delta x \Delta z
+\left[\tau_{zx}+\frac{\partial \tau_{zx}}{\partial z}\frac{\Delta z}{2}\right]\Delta x \Delta y-\left[\tau_{zx}-\frac{\partial \tau_{zx}}{\partial z}\frac{\Delta z}{2}\right]\Delta x \Delta y$$
$\pm p$, $\pm \tau_{xx}$, $\pm \tau_{yx}$ and $\pm \tau_{zx}$ cancel each other and rearranging the remaining terms gives
$$F^{s}_{x}=\left[-\frac{\partial p}{\partial x}+\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{yx}}{\partial y}+\frac{\partial \tau_{zx}}{\partial z}\right]\Delta x \Delta y \Delta z$$
Combining the body and surface forces along the $x-$direction
$$F_{x}=F^{s}_{x}+F^{b}_{x}=\left[-\frac{\partial p}{\partial x}+\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{yx}}{\partial y}+\frac{\partial \tau_{zx}}{\partial z}\right]\Delta x \Delta y \Delta z + \rho f_{x} \Delta x \Delta y \Delta z$$
The $y$ and $z$ component of the forces can be computed using the same way and the right hind side of the momentum equation becomes
$$\textbf{F}=\textbf{F}^{s}+\textbf{F}^{b}=\left[-\nabla p+\nabla\cdot\boldsymbol{\tau}+\rho\textbf{f}\right]\Delta x \Delta y \Delta z \hspace{20pt} (1)$$
The mass of the fluid element:¶
The left hand side of the momentum equation contains the mass and the acceleration of the fluid element. The mass can be written as $\textrm{density}\times \textrm{volume}$
$$m=\rho \Delta x \Delta y \Delta z $$
The acceleration of the fluid element:¶
Acceleration of the fluid element is the total derivative of the velocity field
$\textbf{U}=u\textbf{i}+v\textbf{j}+w\textbf{k}$ is
$$\textbf{a}=\frac{ D\textbf{U}}{D t}=\frac{\partial \textbf{U}}{\partial t}+\textbf{U}(\nabla\cdot\textbf{U})$$
Therefore the left hand side of the equation becomes
$$\rho \frac{D\textbf{U}}{Dt}\Delta x \Delta y\Delta z$$
In above formulation the changes in density is not considered. In order to take the change of density into account we apply the following identity
$$\rho\frac{D\textbf{U}}{Dt}=\rho\frac{\partial \textbf{U}}{\partial t}+\rho\textbf{U}(\nabla \cdot \textbf{U})$$
$$\rho\frac{\partial \textbf{U}}{\partial t}=\frac{\partial (\rho \textbf{U})}{\partial t}-\textbf{U}\frac{\partial \rho}{\partial t}$$
Using the following vector identity
$$\nabla\cdot(\rho\textbf{U}\textbf{U})=\textbf{U}\nabla\cdot(\rho\textbf{U})+\rho\textbf{U}(\nabla \cdot \textbf{U})$$
$$\rho\textbf{U}(\nabla \cdot \textbf{U})=\nabla\cdot(\rho\textbf{U}\otimes\textbf{U})-\textbf{U}\nabla\cdot(\rho\textbf{U})$$
Combining all the above to get the left hand side of the momentum equation
$$\left[\frac{\partial(\rho \textbf{U})}{\partial t}-\textbf{U}\frac{\partial \rho}{\partial t}+\nabla\cdot (\rho \textbf{U}\otimes\textbf{U})-\textbf{U}\nabla\cdot(\rho\textbf{U})\right]\Delta x \Delta y \Delta z$$
If we rearrange this equation
$$\left[\frac{\partial(\rho \textbf{U})}{\partial t}-\textbf{U}\left\{\frac{\partial \rho}{\partial t}+\nabla\cdot(\rho\textbf{U})\right\}+\nabla\cdot (\rho \textbf{U}\otimes\textbf{U})\right]\Delta x \Delta y \Delta z \hspace{20pt} (2)$$
Notice that the term in curly brackets is zero due to continuity equation. Combining equation (1) and (2) ($\Delta x \Delta y \Delta z$ drops out) we can write momentum equation as follows
$$\frac{\partial(\rho \textbf{U})}{\partial t}+\nabla\cdot (\rho \textbf{U}\otimes\textbf{U})=-\nabla p+\nabla\cdot\boldsymbol{\tau}+\rho\textbf{f}\hspace{20pt} (3)$$
Equation (3) is the representation of Newton's second law for fluid flow. The first term is the time rate of change of momentum (density$\times$velocity), the second term is convective acceleration. The right hand side is the sum of forces due to pressure gradient, viscous forces and body forces. From the Stokes's hypothesis the stress tensor is written as follows
$$\boldsymbol{\tau}=\left[\begin{array}{ccc}
\tau_{xx} & \tau_{xy} & \tau_{xz} \\
\tau_{yx} & \tau_{yy} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \tau_{zz}
\end{array}\right]$$
This is a symmetric tensor and the components are
$$\tau_{xx} = 2\mu\frac{\partial u}{\partial x}+\lambda\left[\nabla\cdot\textbf{U}\right]\hspace{10pt},\hspace{10pt}\tau_{yy} = 2\mu\frac{\partial v}{\partial y}+\lambda\left[\nabla\cdot\textbf{U}\right]\hspace{10pt},\hspace{10pt}\tau_{zz} = 2\mu\frac{\partial w}{\partial z}+\lambda\left[\nabla\cdot\textbf{U}\right]$$
$$\tau_{xy}=\tau_{yx}=\mu\left[\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right]\hspace{10pt},\hspace{10pt}\tau_{xz}=\tau_{zx}=\mu\left[\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right]\hspace{10pt},\hspace{10pt}\tau_{yz}=\tau_{zy}=\mu\left[\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right]$$
In here $\lambda$ is the bulk viscosity and it is equal to
$$\lambda=-\frac{2}{3}\mu$$
INCOMPRESSIBLE CASE:¶
Lets rewrite the left hand side of equation (3) using vector identities
$$\rho\frac{\partial \textbf{U}}{\partial t}+\textbf{U}\frac{\partial \rho}{\partial t}+\rho\nabla\cdot(\textbf{U}\otimes\textbf{U})+(\textbf{U}\otimes\textbf{U})\cdot\nabla\rho$$
For incompressible flow the density is assumed to be constant, therefore the second and fourth term in the above equation drops out, the left hand side becomes
$$\rho\frac{\partial \textbf{U}}{\partial t}+\rho\nabla\cdot(\textbf{U}\otimes\textbf{U})$$
Now expanding the tensor product as follows
$$\textbf{U}\otimes\textbf{U}=\left[\begin{array}{ccc}
uu & uv & uw \\
vu & vv & vw \\
wu & wv & ww
\end{array}\right]$$
and the divergence of this product becomes
$$\nabla \cdot\left[\begin{array}{ccc}
uu & uv & uw \\
vu & vv & vw \\
wu & wv & ww
\end{array}\right]=\left[\frac{\partial uu}{\partial x}+\frac{\partial vu}{\partial y}+\frac{\partial wu}{\partial z}\right]\textbf{i}+\left[\frac{\partial uv}{\partial x}+\frac{\partial vv}{\partial y}+\frac{\partial wv}{\partial z}\right]\textbf{j}+\left[\frac{\partial uw}{\partial x}+\frac{\partial vw}{\partial y}+\frac{\partial ww}{\partial z}\right]\textbf{k}$$
Using the product rule for the derivation;
$$\frac{\partial uu}{\partial x}+\frac{\partial vu}{\partial y}+\frac{\partial wu}{\partial z}=u\frac{\partial u}{\partial x}+u\frac{\partial u}{\partial x}+u\frac{\partial v}{\partial y}+v\frac{\partial u}{\partial y}+u\frac{\partial w}{\partial z}+w\frac{\partial u}{\partial z}=u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}+u[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}]$$
$$\frac{\partial uv}{\partial x}+\frac{\partial vv}{\partial y}+\frac{\partial wv}{\partial z}=u\frac{\partial v}{\partial x}+v\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}+v\frac{\partial v}{\partial y}+v\frac{\partial w}{\partial z}+w\frac{\partial v}{\partial z}=u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}+v[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}]$$
$$\frac{\partial uw}{\partial x}+\frac{\partial vw}{\partial y}+\frac{\partial ww}{\partial z}=u\frac{\partial w}{\partial x}+w\frac{\partial u}{\partial x}+w\frac{\partial v}{\partial y}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}+w\frac{\partial w}{\partial z}=u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}+w[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}]$$
The last terms in the above equations are zero due to incopmressible continuity equation ($\nabla \cdot \textbf{U}=0$) therefore the left hand side of equation (3) for incompressible flows becomes
$$\rho\frac{\partial \textbf{U}}{\partial t}+\rho\textbf{U}\cdot(\nabla\otimes\textbf{U})$$
Now consider the right hand side of the equation (3). The pressure gradient and the body force terms are not related to the incompressibility condition. But the viscous stress tensor changes for constant density due to the incompressibility condition ($\nabla\cdot\textbf{U}=0$) and the tensor components in normal direction become
$$\tau_{xx} = 2\mu\frac{\partial u}{\partial x}\hspace{10pt},\hspace{10pt}\tau_{yy} = 2\mu\frac{\partial v}{\partial y}\hspace{10pt},\hspace{10pt}\tau_{zz} = 2\mu\frac{\partial w}{\partial z}$$
$$\nabla \cdot \boldsymbol{\tau}=\left[\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{xy}}{\partial y}+\frac{\partial \tau_{xz}}{\partial z}\right]\textbf{i}+\left[\frac{\partial \tau_{yx}}{\partial x}+\frac{\partial \tau_{yy}}{\partial y}+\frac{\partial \tau_{yz}}{\partial z}\right]\textbf{j}+\left[\frac{\partial \tau_{zx}}{\partial x}+\frac{\partial \tau_{zy}}{\partial y}+\frac{\partial \tau_{zz}}{\partial z}\right]\textbf{k}$$
Writing the $x$ component part in detail:
$$\left[\frac{\partial \tau_{xx}}{\partial x}+\frac{\partial \tau_{xy}}{\partial y}+\frac{\partial \tau_{xz}}{\partial z}\right]=\frac{\partial}{\partial x}\left[2\mu\frac{\partial u}{\partial x}\right]+\frac{\partial }{\partial y}\left[\mu\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right]+\frac{\partial }{\partial z}\left[\mu\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)\right]$$
$$\hspace{30pt}=2\mu\frac{\partial^{2}u}{\partial x^{2}}+\mu\frac{\partial ^{2}u}{\partial y^{2}}+\mu\frac{\partial^{2}v}{\partial x\partial y}+\mu\frac{\partial^{2}u }{\partial z}+\mu\frac{\partial^{2} w}{\partial x\partial z}$$
$$\hspace{51pt}=\mu\left[\frac{\partial^{2}u }{\partial x^{2}}+\frac{\partial^{2}u }{\partial y^{2}}+\frac{\partial^{2}u }{\partial z^{2}}\right]+\mu\frac{\partial}{\partial x}\left[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\right]$$
The viscosity $\mu$ is also considered as constant and came out of the derivation. Again the second terms is zero because of the incompressibility. The $y$ and $z$ components can be derived in same way and the force term due to viscous stress is written as follows
$$\nabla \cdot \boldsymbol{\tau}=\mu \nabla^{2}\textbf{U}$$
Finally the momentum equation (3) for incompressible flows becomes
$$\rho\frac{\partial \textbf{U}}{\partial t}+\rho\textbf{U}\cdot(\nabla \otimes \textbf{U})=-\nabla p + \mu \nabla^{2}\textbf{U}+\rho \textbf{f}$$
$x$ direction:
$$\rho\frac{\partial u}{\partial t}+\rho (\textbf{U}\cdot\nabla)u=-\frac{\partial p}{\partial x} + \mu \nabla^{2}u+\rho f_{x}$$$y$ direction:
$$\rho\frac{\partial v}{\partial t}+\rho (\textbf{U}\cdot\nabla)v=-\frac{\partial p}{\partial y} + \mu \nabla^{2}v+\rho f_{y}$$$z$ direction:
$$\rho\frac{\partial w}{\partial t}+\rho (\textbf{U}\cdot\nabla)w=-\frac{\partial p}{\partial z} + \mu \nabla^{2}w+\rho f_{z}$$<< 2.2 Conservation of Mass || Contents || 2.4 Conservation of Energy >>
References:
[1] Computational Fluid Dynamics, J.D. Anderson, McGraw-Hill Education, 1995.
[2] An Introduction to Computational Fluid Dynamics, H.K. Versteeg and W. Malalasekera, Pearson Education Limited, 2007.