VISCOELASTIC FLUID FLOW INSTABILITIES
Prediction and suppression of the onset of viscoelastic
fluid flow instabilities are of great importance in many industrial polymer
processing applications where output quality constraints require that operating conditions should
be maintained in the stable flow regime. Therefore, the flow instabilities
are the primary constraint for the processing speed in many industrial polymer
forming processes such as extrusion, wire coating, blow molding,
sheet-formation, etc. These viscoelastic instabilities occur in the creeping
motion of non-Newtonian polymeric liquids and are entirely absent in the
corresponding motion of Newtonian liquids. A parallel
stable unstructured finite volume algorithm Visco-Solve has been developed
in order to investigate the viscoelatic fluid flow instabilities. The
numerical method is based on the side-centered finite volume method where
the velocity vector components are defined at the mid-point of each cell
face, while the pressure term and the extra stress tensor are defined at
element centroids. The present arrangement of the primitive variables leads
to a stable numerical scheme and it does not require any ad-hoc modifications
in order to enhance the pressure-velocity-stress coupling. The log-conformation
representation has been implemented in order improve the limiting Weissenberg
numbers. The time stepping algorithm used decouples the calculation of the
polymeric stress by solution of a hyperbolic constitutive equation from the
evolution of the velocity and pressure fields by solution of a generalized
Stokes problem. The resulting algebraic linear systems are solved using the
FGMRES(m) Krylov iterative method with the restricted additive Schwarz
preconditioner for the extra stress tensor and the geometric non-nested multilevel
preconditioner for the Stokes system. The calculations are presented for
an Oldroyd-B fluid past a confined circular cylinder in a rectangular channel
at relatively high Weissenberg numbers. The present numerical calculations
reveal three-dimensional purely-elastic instabilities in the wake of a confined
single cylinder which is in accord with the earlier experimental results
in the literature. In addition, the flow field is found out to be no longer
symmetric in the wake of the cylinder at high Weissenberg numbers.
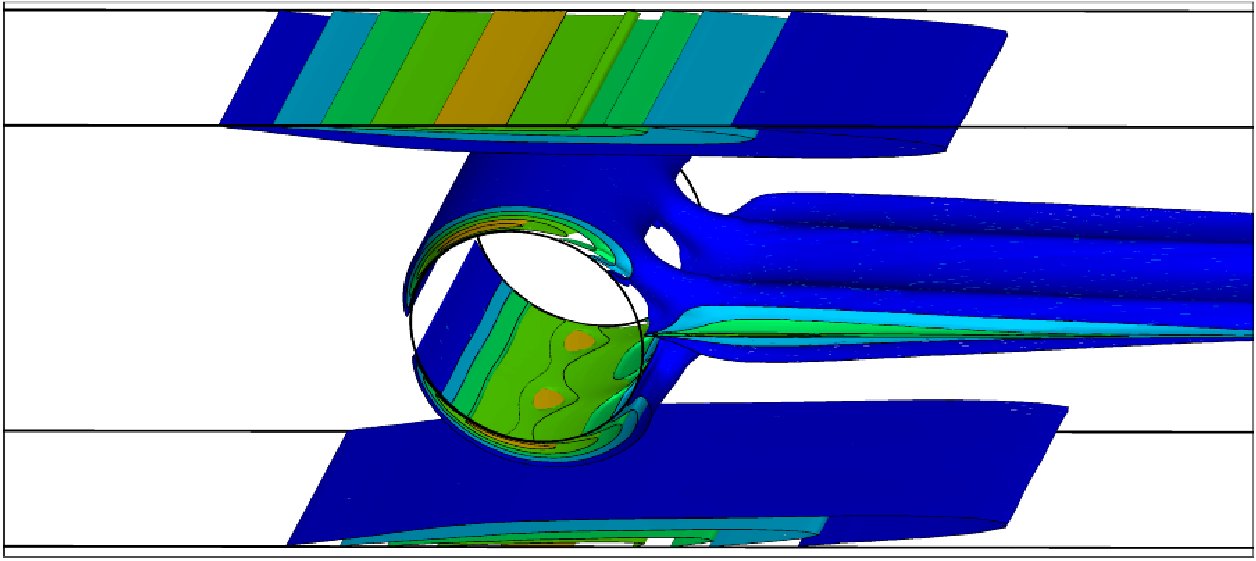
The computed Txx contours around a confined circular cylinder in a channel with D/H=0.5 at We=2.0 and Re=0.0 for an Oldroyd-B fluid.
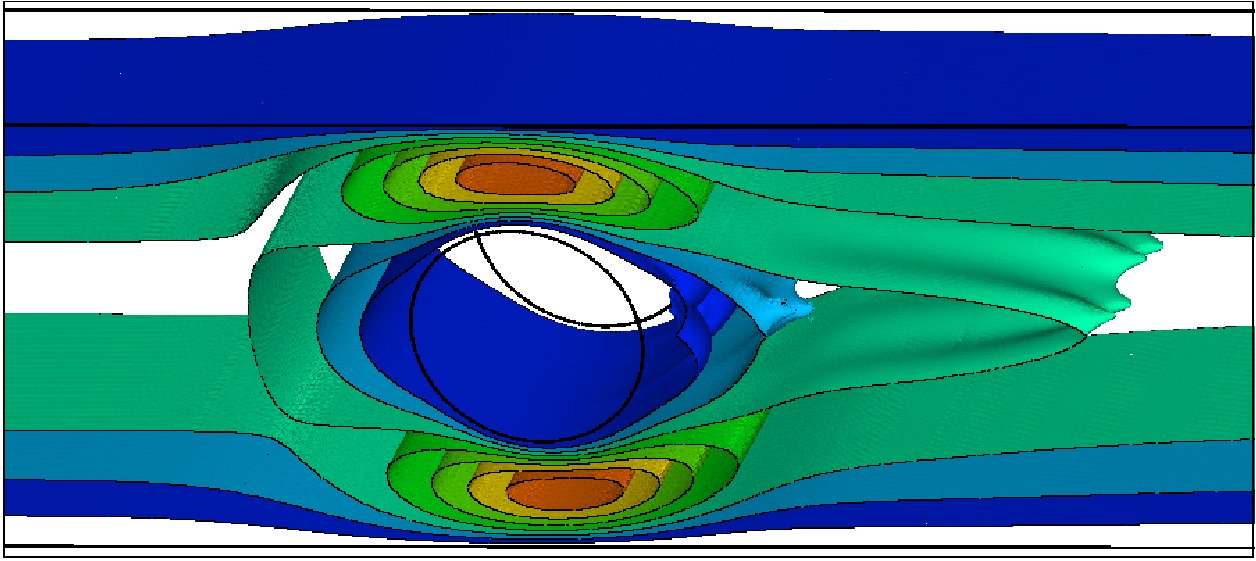
The computed u-velocity contours around a confined circular cylinder in a channel with D/H=0.5 at We=2.0 and Re=0.0 for an Oldroyd-B fluid.
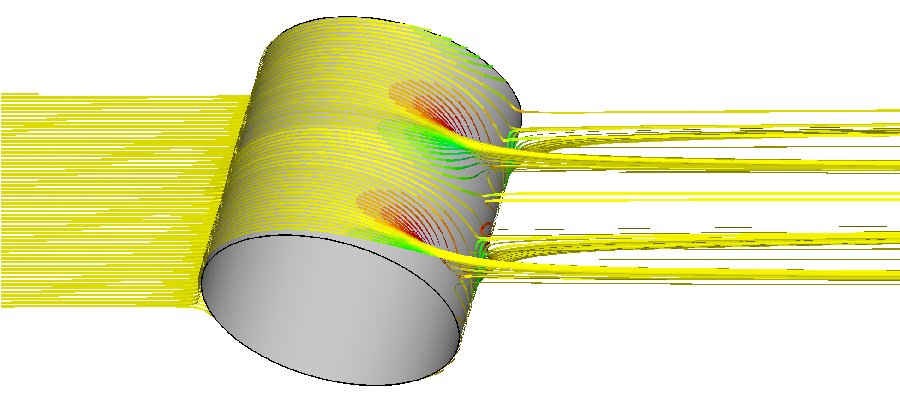 [a]
[a]
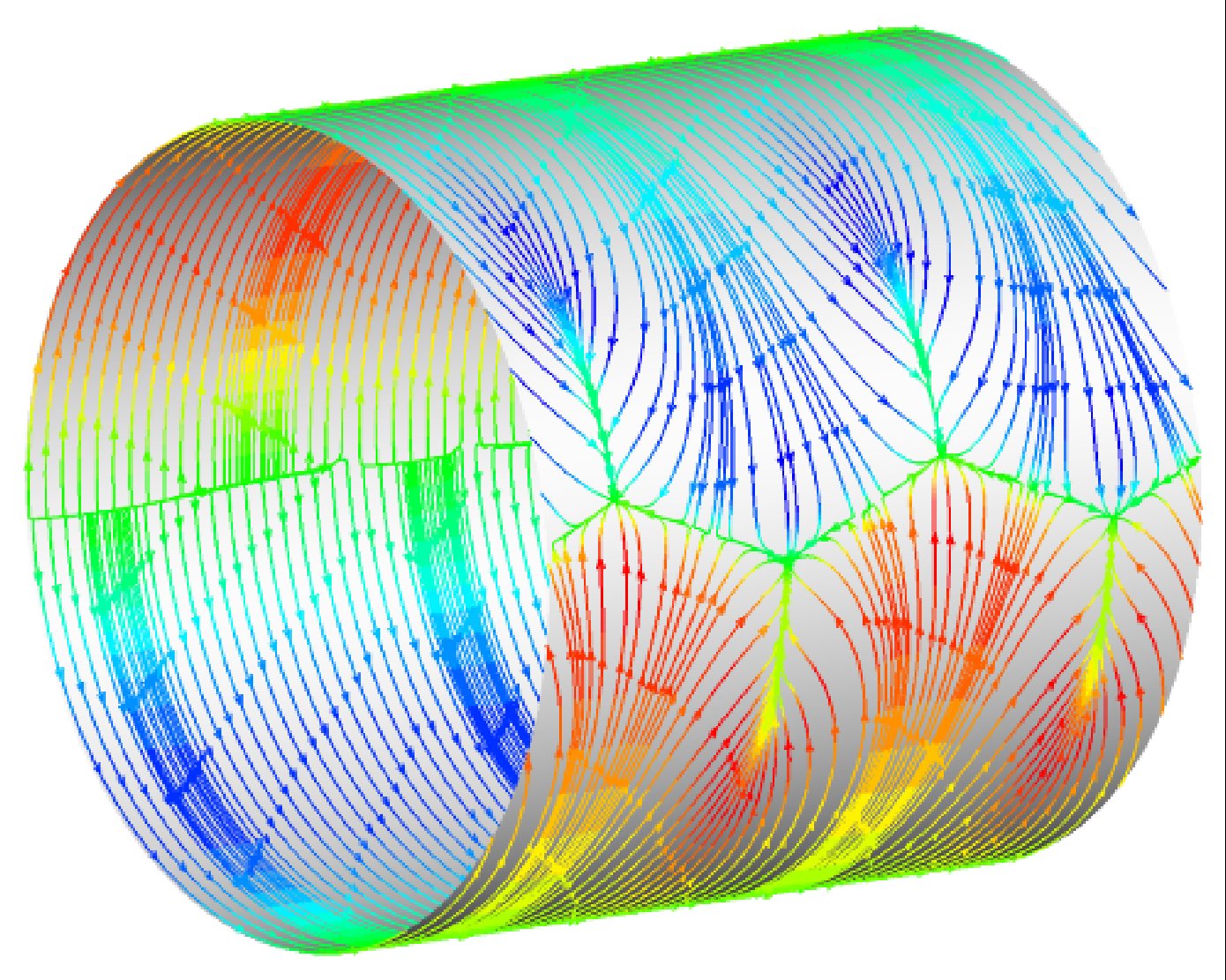 [b]
[b] The compted streamtraces around a confined circular cylinder [a] and the surface streamlines indicating separation lines [b] at We=2.0 and Re=0.0 for an Oldroyd-B fluid . The calculations reaveal three-dimensional viscoelastic wake instability.