THE NUMERICAL INVESTIGATION OF NEAR WAKE STRUCTURES FOR ANIMAL LOCOMOTIONS
A parallel large-scale unstructured
finite volume algorithm based on an arbitrary Lagrangian-Eulerian (ALE)
formulation has been developed in order to investigate the near wake structure
of the swimming/flying animals. In the ALE method, the mesh follows the
interface between the fluid and solid boundary and the governing equations
are discretized on unstructured moving meshes. This differs
from the standard Eulerian formulation in a way that the
mesh movement has to fulfill special conditions in order to maintain
the accuracy and the stability of the time integration scheme.
This condition is satisfied by the enforcement of the so-called
discrete geometric conservation law (DGCL). The mesh deformation
algorithm is based on either the indrect implementaion of radial basis
function (RBF) or the solution of the elasticity equations. For
the parallel solution of resulting large-scale algebraic equations in
a fully coupled form, a matrix factorization is introduced similar to
that of the projection method for the whole system and two-cycle of BoomerAMG
solver is used for the scaled discrete Laplacian provided by the HYPRE
library which we access through the PETSc library.The numerical algorithm
is used to study the time-variation of the Eulerian
and Lagrangian chorent structures in the near wake.


Three dimensional wake structure behind a free-swimming hydromedusa Aequorea victoria (crystal jelly).
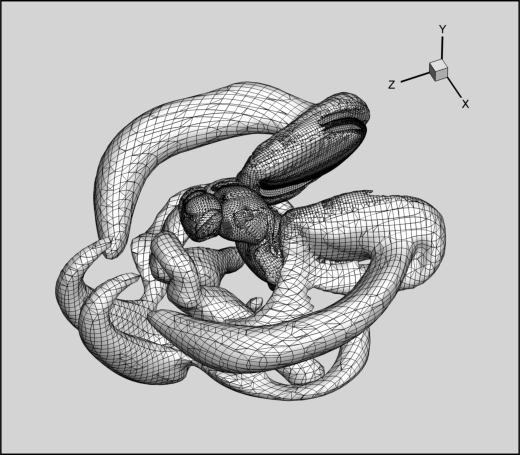
Three dimensional near wake structure around the flapping Drosophila (E. Dilek and B.Erzincanli).