DOĞANIN GEOMETRİSİ: FRAKTAL GEOMETRİ

Matematiğin önemli bir kolu olarak geometri, insanoğlunun doğayı nasıl algıladığı ile yakından ilişkilidir. Algılama biçimleri geliştikçe, daha ileri geometrik yaklaşımlar ortaya konmuştur. Bir mağara duvarına çizilen resimler bile belli bir geometrik yaklaşımı yansıtmaktadır. Diğer bir deyişle mağara duvarına resim yapan kişi, örneğin bir boğayı en azından belli bir oranda küçülterek çizmesi gerektiğini bilmektedir.

Yerleşik hayata geçilmesiyle  geometrinin önemi ve geometriye duyulan gereksinim daha da artmıştır. Tarihte Mısırlılar ve Babilliler geometriye önemli katkılar yapmışlardır. Eski Mısır’da Nil Nehri’nde meydana gelen peryodik taşkınlar tarla sınırlarını ortadan kaldırıyordu. Durum normale döndükten sonra tarla sınırlarının yeniden belirlenmesi gerekmekteydi. Mısırlılar bu sorunun üstesinden  geometri bilgisini kullanarak gelmeyi başardı.  Diğer taraftan Mısır matematiğine ilişkin araştırmalar, Mısırlıların hem küre yüzeyini hem de kesik piramidin hacmini bildiklerini göstermektedir. Babilliler ise arazi ölçümü yapabiliyor ve ikinci dereceden denklemleri çözebiliyordu.  

 Euclides geometrisi 2000 yıldan fazla bir zamandır  hakimiyetini sürdürmektedir. Bu klasik geometri anlayışında doğada karşımıza çıkan şekiller; doğrular ve düzlemler, daireler ve küreler, üçgenler ve koniklerden ibarettir. Bu şekiller gerçeğin güçlü bir soyutlamasından ibarettir.  Doğada var olan karmaşık yapıyı anlamak ve modelleyebilmek için yukarıda bahsedilen soyut  şekillerin yeterli olmadığı artık  bilinen bir gerçektir.

 Yakından incelendiğinde doğadaki nesnelerin Euclides geometrisindeki şekillere hiç benzemediği görülecektir.  Tam küre şeklinde olan bir tane bile elma ya da bulut bulunamaz veya tam koni şeklinde olan bir dağ hiç bir zaman yeryüzünde olmadı. Benzer şekilde doğada gövdesi silindir şeklinde olan bir ağaca, bir hat boyunca ilerleyen yıldırıma ya da tepsi gibi düz bir ovaya rastlanamaz.  Özetle doğayı daha iyi anlayabilmek ve modelleyebilmek için yeni bir  geometriye gereksinim vardır.

 Yukarıda sözü edilen yeni geometrinin adı “ fraktal geometri”dir.  Bu isim Fransız bilim adamı Benoit Mandelbrot tarafından verilmiştir. “Fraktal” kelimesi Latince “fraktus (kırık taş)” kelimesinden türetilmiştir. Fraktal geometrinin yarattığı evren, yuvarlak veya düz olmayan; girintili çıkıntılı, kırık, bükük, birbirine girmiş, düğümlenmiş vb şekillerden oluşan bir evrendir. Bu evren Euclid geometrisinin tasvir ettiği türden sıkıcı ve tekdüze bir evren değildir; tersine gözlemciye her ölçekte ayrı bir dünyanın kapılarını aralar. Fraktal bir nesneye bakan gözlemci, matematikdeki “sonsuz” kavramının nasıl somuta dönüştüğüne tanık olur.

 Fraktal bir şeklin neye benzediğini daha iyi anlayabilmek için Mandelbrot’un  İngiltere sahilleri için sorduğu soruyu biz Türkiye sahilleri için sorarak başlayalım: “Türkiye sahillerinin toplam uzunluğu nedir?” Mandelbrot’un iddiasına göre,  her sahil  bir bakıma sonsuz uzunluktadır, diğer bir deyişle, sorunun cevabı kullanılan cetvelin uzunluğuna bağlıdır. Örneğin açıklığı bir metre olan bir pergel ile Türkiye sahillerinin uzunluğu ölçüldüldüğünde, bulunan değer yaklaşık bir tahminden ibaret olacaktır. Çünkü pergel bir metrenin altındaki girinti ve çıkıntıların üzerinden atlayacaktır. Pergel açıklığı yarım metreye indiğinde, bu uzunluk ölçeğindeki ayrıntılar da hesaba katılmış olacaktır.  Dolayısı ile daha  hassas bir ölçüm için her seferinde pergel açıklığını biraz daha küçültmemiz gerekecektir. Sonuçta bulmuş olduğumuz sahil uzunluğu, kullanılan uzunluk ölçeğine bağlı olacaktır. Örneğin bir uydudan ölçülen Türkiye sahillerinin uzunluğu, bütün koyları ve burunları adımlayarak ölçüm yapan bir gözlemcinin bulduğu uzunluktan daha küçük bir değer olacaktır.

 Eğer sahil Euclides geometrisindeki şekillerden birine örneğin bir daireye benzeseydi, gittikçe küçülen pergel açıklıklarıyla yapılan ölçümler sonuçta belli bir değere yakınsardı. Ancak fraktal yaklaşıma göre, ölçek küçüldükçe bulunan sahil uzunluğu sürekli olarak artacak; körfez ve yarımadalardan daha küçük körfezcikler ve yarımadacıklar ortaya çıkacak ve bu işlem ancak atom boyutuna ulaşıldıktan sonra sona erecektir, çünkü sahillerin yapısında fraktallik mevcuttur. Bu yapıyı geometrik olarak tam tanımlı Koch eğrisine benzetebiliriz. Aşağıda nasıl elde edildiği adım adım anlatılan Koch eğrisi bir sahil için ideal bir model oluşturmaktadır (Şekil 1).

 Şekil 1’de görüldüğü gibi A0 adımında birim uzunlukta bir doğru parçası ile başlayıp A1 adımında her biri 1/3  birim uzunluğundaki 4 doğru parçasından yeni bir şekil elde edilir. Bunu yaparken orta 1/3’lük parça atılıp, onun yerine aynı uzunlukta iki parça eklenir. Bu şekilde her yeni adımda, bir önceki adımda elde edilen doğru parçalarına aynı işlem uygulanınca sonuçta fraktal bir şekil ortaya çıkar. İşleme bu şekilde devam edilip n. adıma gelinirse eğrinin toplam uzunluğu (4/3) ⁿ olacaktır. Eğer n yeterince büyük alınırsa eğrinin uzunluğu da sonsuza gidecektir. Diğer bir deyişle Koch eğrisinde iki nokta arasındaki uzaklık sonsuzdur. Eğer bu eğri yakından incelenirse şeklin tamamı ile onu oluşturan alt parçaların bir birine benzer olduğu görülür. Örneğin şeklin tamamını 3 kat küçültürseniz bir alt parçasını elde edersiniz. Bu küçültme işlemine sonsuza kadar devam edebilirsiniz.

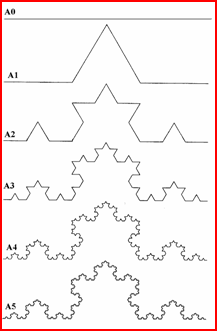
 Şekil 1: Koch eğrisinin oluşturulması

Bu aşamada artık bir fraktal şeklin tanımını yapabiliriz: Bir fraktal şekil kendi kendine benzer parçalardan oluşmuş bir şekildir. Fraktal şekillerin diğer önemli bir özelliği de boyutlarıdır. Bilindiği gibi Euclides geometrisindeki bütün şekiller tam sayı bir boyuta sahiptir. Örneğin noktanın boyutu 0, doğrunun boyutu 1, karenin boyutu 2, kübün boyutu 3’dür. Oysa fraktal şekiller tam sayı bir boyutla temsil edilemezler (Şekil 2). Koch eğrisi  iki nokta arasında sonsuz uzunlukta olması nedeniyle basit bir doğrunun ötesine taşmakta, diğer taraftan bir düzlemi de tam olarak dolduramamaktadır. Öyleyse Koch eğrisinin boyutu 1 ile 2 tam sayıları arasında yani kesirli bir sayı olmalıdır. Koch eğrisinin boyutu 1.26’dır. Bu örnekte olduğu gibi kesirli bir boyutlara fraktal boyut denir.

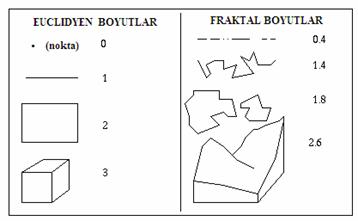
Şekil 2: Euclidyen ve Fraktal boyutların karşılaştırılması.

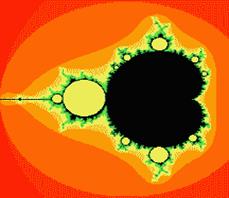
Çeşitli matematiksel fonksiyonların ardışık olarak çözülmesi sonucu son derece büyüleyici fraktal şekiller elde edilebilmektedir (Şekil 3, 4). Daha önce bir sahilin fraktal yapıya sahip olduğu üzerinde durulmuştu. Yalnızca sahiller değil,  doğanın her hangi bir parçası, adaların dağılımı, dağlar, bir havzadaki ana akarsu ve kollarının oluşturduğu şekil, buzullar, belli bir kristal yapının veya tanenin bir kaya içindeki dağılımı, bitkilerin geometrisi vb fraktal özelliktedir.  Şekil 5 ve 6 yakından incelenirse fraktal yaklaşımın doğayı son derece gerçekçi bir şekilde yansıttığı görülecektir.

Şekil 3: Julia kümesi                                  Şekil 4: Mandelbrot kümesi

Şekil 5: Eğrelti otu                      Şekil 6: Fraktal manzara