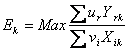ITU İşletme Fakültesi

ISL506—MATEMATİKSEL PROGRAMLAMA

VERİ ZARFLAMA ANALİZİ (VZA)

Belirli bir çıktı bileşimini en etkin şekilde üretebilmek amacıyla kullanılacak en uygun girdi bileşiminin nasıl olması gerektiğini araştıran modellere girdiye yönelik VZA Modelleri denir.

Oransal VZY modeli:

Bu modelde;

E_k = k karar biriminin etkinliği

u_r = k karar birimi tarafından r’inci çıktıya verilen ağırlık

v_i = k karar birimi tarafından i’inci girdiye verilen ağırlık

Y_rk = k’ıncı karar birimi tarafından üretilen r’inci çıktı

X_ik = k’ıncı karar birimi tarafından kullanılan i’inci girdi

Y_rj = j’inci. karar birimi tarafından üretilen r’inci çıktı

X_ij = j’inci karar birimi tarafından kullanılan i’inci girdi

ε   = Yeterince küçük pozitif bir sayı (Örneğin 0,0001)

n   =  Karar birimi sayısı

t    = Çıktı sayısı

m  = Girdi sayısı

Yukarıdaki oransal VZA modelinin amaç fonksiyonundan görüldüğü üzere, gözlem kümesindeki her bir karar birimi göz önüne alınarak diğer gözlemlerle karşılaştırmalı etkinlik düzeyi ölçülmektedir. Etkinlik ölçütü (E_k), karar birimi için ağırlıklı çıktıların ağırlıklı girdilere oranı şeklinde tanımlanmaktadır. Kısıt kümesine bakıldığında, amaç fonksiyonu ile seçilen karar birimi için etkinlik ölçütü en yüksek kılınmaya çalışılırken, aynı ölçütün (oranın) diğer karar birimleri açısından da 1’den küçük ya da 1’e eşit olması koşulu göz önünde bulundurulmaktadır. Model aracılığıyla, göreli etkinliği ölçülen karar birimi için girdi-çıktı ağırlık vektörlerinin (u,v) değerleri hesaplanır. Ayrıca bu değerlerin “yeterince küçük pozitif bir sayı olan” ε’dan büyük ya da eşit olması şartı vardır. Bu koşul aracılığıyla, herhangi bir girdi ya da çıktı bileşeninin ağırlıklarını belirleyen u_r ve v_i değerlerinin 0’a eşitlenmesi engellenmeye çalışılmaktadır.

GİRDİYE YÖNELİK VZA MODELLERİ

<<Geri

İleri>>

Etkinlik seviyesi 1 olan karar merkezi, etkin kenarı (efficient frontier) oluşturarak diğer karar birimlerini “zarflar”.

KAYNAKLAR

Yolalan, R. (1993). İşletmeler Arası Göreli Etkinlik Ölçümü. Milli Prodüktivite Merkezi Yayınları: 483, Ankara.

CHARNES, A. COOPER, W.W. ve RHODES, E., LEWIN A.Y., VE SEIFORD L.M. (1994), Data Envelopment Analysis: Theory, Methodolohy, and Application, Boston, Kluwer  Academic Pub.