Ross S. Stein ¹, Aykut A. Barka ² and James H. Dieterich ¹

1 U.S. Geological Survey, MS 977, Menlo Park, CA 94025 USA (rstein@usgs.gov; jdieterich@usgs.gov)

2 Istanbul Technical University, Department of Geology, Istanbul, 80626 Turkey (barka@sariyer.cc.itu.edu.tr)

SUMMARY

Ten M>=6.7 earthquakes ruptured 1,000 km of the North Anatolian fault (Turkey) during 1939-92, providing an unsurpassed opportunity to study how one large shock sets up the next. We use the mapped surface slip and fault geometry to infer the transfer of stress throughout the sequence. Calculations of the change in Coulomb failure stress reveal that 9 out of 10 ruptures were brought closer to failure by the preceding shocks, typically by 1-10 bars, equivalent to 3-30 years of secular stressing. We translate the calculated stress changes into earthquake probability gains using an earthquake-nucleation constitutive relation, which includes both permanent and transient effects of the sudden stress changes. The transient effects of the stress changes dominate during the mean 10-year period between triggering and subsequent rupturing shocks in the Anatolia sequence. The stress changes result in an average three-fold gain in the net earthquake probability during the decade after each event. Stress is calculated to be high today at several isolated sites along the fault. During the next 30 years, we estimate a 15% probability of a M>=6.7 earthquake east of the major eastern center of Ercinzan, and a 12% probability for a large event south of the major western port city of Izmit. Such stress-based probability calculations may thus be useful to assess and update earthquake hazards elsewhere.

Key words: stress triggering, stress transfer, earthquake sequence, earthquake nucleation, hazard assessment, Izmit, Erzincan, Istanbul

INTRODUCTION

Like falling dominoes, four westward-migrating earthquakes ruptured 725 km of the North Anatolian fault during 1939-44, with subsequent earthquakes extending the zone of faulting eastward and westward (Fig. 1). This classic case of progressive earthquake failure has tantalized earth scientists (Allen, 1969; Dewey, 1976; Jackson & McKenzie, 1988; Richter, 1958; Scholz, 1990) , and terrorized insurance providers, for half a century. Although clustering of earthquakes in space and time is common (Dieterich, 1994; Kagan & Jackson, 1991) , and migrating earthquake sequences have occurred elsewhere (Kasahara, 1981; Mogi, 1985) , none is as spectacular as on the North Anatolian fault. Most recently, Roth (1988) modeled the shear stress buildup along the western part of the North Anatolian fault using a simple fault geometry with collinear ruptures of uniform slip, and found that the stress at future ruptures was generally raised by the preceding events.

New observations of the North Anatolian fault, as well as new methods to calculate how seismic stress transfer alters the probability of subsequent earthquakes, encourage us to revisit this sequence to learn what conditions promote progressive failure. Until recently, the fault geometry was poorly known, and there were few measurements of the 1939-44 earthquake fault slip (Ambraseys, 1970; Ketin, 1969) , precluding calculation of the earthquake-induced stresses. Nor could the stress transferred by the steady or 'secular' stress accumulation be calculated, since the rate of deep fault slip driving the stress buildup was uncertain by a factor of four (Barka, 1992; Jackson & McKenzie, 1988; Le Pichon, et al., 1993) . New findings remove these obstacles: A threefold increase in measurements of earthquake slip, including a twelve-fold increase for the largest 1939 shock (Barka, 1995) provides data essential to model the earthquake stress changes (Fig. 1b). New detailed fault mapping (Barka, 1992; Saroglu & Kusçu, 1992) (Fig. 1c) reduces the uncertainty in the fault location from about ±25 km to ±5 km. Finally, geodetic analyses yield the slip rate along the fault (Oral, 1994; Straub & Kahle, 1994; Straub, 1996) .

The North Anatolian fault emerges as a close analogue of the San Andreas fault in California, with the two continental transforms sharing similar slip rates, total length, and straightness relative to their poles of rotation (Fig. 1a). But while the San Andreas fault produced just two M>=6.7 earthquakes in this century (in 1906 and 1989), the North Anatolian fault has suffered ten such shocks, thus providing a superior natural laboratory to study earthquake interaction (Fig. 1b-c). Ruptures from Parkfield to the Salton Sea within 5 yr would, for example, be a comparable sequence on the San Andreas fault. We find that all but one earthquake increased the stress toward failure at the site of the subsequent shocks, and inhibited failure on most fault segments which did not rupture. We argue that the calculated several-bar stress increases raised the earthquake probability three-fold during the ensuing decade, and we suggest why migrating earthquake sequences are prevalent on the North Anatolian fault. Bolstered by recent findings that aftershocks and background seismicity concentrate where the stress has risen (Harris & Simpson, 1992; Harris, et al., 1995; Jaumé & Sykes, 1992; King, et al., 1994; Stein, et al., 1994; Jaumé & Sykes, 1996) , these results offer a new approach to updatable forecasts of earthquake hazard.

COULOMB FAILURE STRESS CHANGE

We calculate the static Coulomb stress changes resulting from North Anatolian ruptures since 1939, with stress calculated in an elastic halfspace at all points (as shown in Figs. 3b, 4 and 5) or resolved on the fault plane (as listed in the tables and shown in Fig. 3a). Since we lack hypocentral depths for the Anatolian main shocks, we sample stress in the central part of the seismogenic crust at a depth of 8 km. Failure is facilitated on a plane when the Coulomb failure stress sf rises

,

(1)

where is the shear stress on the failure plane b (positive in the direction of fault slip) and sb' is the effective normal stress (positive in compression); ms'b ª m'sb, where m' is the apparent coefficient of friction with range 0.0-0.75. The confining stress can be related to fluid pore pressure by Skempton's coefficient, B, the ratio of the change in pore pressure in a cavity to the change in applied stress, where m' = m(1-B) (Roeloffs, 1988) . Immediately after the earthquake, B ª 2/3, but could fall to zero if fluids were to drain fully from the fault zone (Scholz, 1990) . We set m'=0.4; equivalent to laboratory values of friction (m~0.75) and moderate pore pressure if fluids are not fully expelled (B~0.5), or to a low value of friction as inferred for the San Andreas fault (Zoback et al., 1987) . A m' of 0.4 also minimizes the calculation error caused by the uncertainty in m' to ±25% (King, et al., 1994) ; compare, for example, col. 2 (for m' = 0.75) and col. 3 (for m' = 0.40) in Table 2.

Secular stress change

In addition to earthquakes, steady slip beneath the North Anatolia fault system transfers stress to the seismogenic portion of the fault. This we model with slip tapering from 0 at 12.5-km depth to the full rate below 24 km (Fig. 2a). GPS data give 24±4 mm/yr along the North Anatolian fault (Oral, 1994) ; near its western end, slip is partitioned with 16 mm/yr along the Karamürsel-Sapanca faults and 9 mm/yr along the Iznik-Geyve faults (Straub & Kahle, 1994; Straub, 1996) . GPS data also resolve left-lateral slip of 18±6 mm/yr on the East Anatolian fault and ~5 mm/yr on the Northeast Anatolian fault (Bennett, et al., 1996; Oral, 1994) (Fig. 1c and Fig. 2). During a complete earthquake cycle in this model, coseismic slip would take place over 0-12.5 km and secular slip over 12.5-100 km. Such a model will not produce uniform stress even when averaged over many earthquake cycles, since the fault strike and coseismic slip are both variable (Fig. 1b). In addition, we neglect postseismic slip beneath 12.5 km, so we likely underestimate the total stress transfer during the cycle.

Shear stress builds in this model at 0.15 bar/yr along most of the North Anatolian fault (Fig. 2b). Because uniform right-lateral slip is imposed beneath a relatively straight North Anatolian fault at depth, appreciable normal stress is transferred to the fault at seismogenic depths only at fault bends (such as at km = -350 to -400, or km 500-550). A uniform stress increase of 0.01 bar/yr is added at all points to account for the small residual stressing on faults more than 100 km from Anatolia fault system. (Fig. 1a). This small addition stress keeps the secular stress buildup positive at all sites in the model.

Resolved and optimally-oriented stress changes

The Coulomb stress change caused by the 1939 earthquake is resolved on major faults in Fig. 3a. Shear and normal stress is resolved on the fault surface, (projected in UTM coordinates) at a depth of 8 km. Faults are assumed to be vertical and to slip in the sense indicated by the arrows, except for the west end of the 1939 rupture, which dips 50°N and has oblique reverse slip. The apparent coefficient of friction, m', is assumed to be 0.4; no information about the regional stress is needed for this calculation. The Coulomb stress is seen to drop by 50-100 bars along most of the 1939 rupture, with increases of several bars along the west end, beyond the east end, and along most of the succeeding 1942 fault rupture zone. The resolved stress changes are sensitive both to position and fault strike. Note that a right-lateral Coulomb stress of 100 bars is not equivalent to a left-lateral Coulomb stress of -100 bars on the same fault unless m'=0, because unlike the shear stress change, the sign of the normal stress change is the same for right- or left-lateral slip (e.g., fault-normal tension always favors failure). Thus the resolved stresses depends on inferring the sense of slip on each fault correctly. This result for the 1939 rupture, and for all succeeding events, is summarized in Tables 1-4.

The Coulomb stress change on optimally oriented vertical strike-slip faults (King, et al., 1994) is plotted in Fig. 3b at a depth of 8 km. To create such a map, one must impose an orientation, and to a lesser extent, magnitude, of the regional (or tectonic) stress, sr. Here we assume a 100-bar uniaxial compression oriented 55° clockwise from the fault as shown by the white opposed arrows in Figs. 2b and 4a. About a dozen sites along the North Anatolian fault exhibit geologic indicators of the orientation of the principal compression axis (Andrieux, et al., 1995; Neugebauer, 1995; Suzanne, et al., 1990); they average 58° relative to the local strike of the North Anatolian fault. The principal strain-rate axes (Oral, 1994) measured geodetically from the Marmara Sea to the central 1939 rupture zone indicate an axis oriented 48° clockwise from the fault. We use a weighted average of these observations. Dynamic models (Gülen, et al., 1987; Kasapoglu & Toksöz, 1983), which consider the stresses imparted to the North Anatolian fault by remote plate tractions, yield a similar orientation.

The principal stresses are calculated from the tensor addition of the 100-bar regional stress, the earthquake stress change, and the secular stress, at every calculation point. Optimal planes are then calculated relative to the local principal stress axes. The internal angle between the right and left plane is a function of the apparent friction coefficient; the planes are orthogonal for m' = 0. Once the optimal planes are obtained, the earthquake plus secular stress changes are resolved on them. We thus calculate the change in Coulomb stress on planes that are optimally oriented after the earthquake. At any given point, the Coulomb stress change along the optimum right- and left-lateral planes is the same (the black and gray planes, respectively, in Figs. 2b and 3b).

The earthquake stress change causes the optimum planes to rotate from the orientation imposed by the regional stress. In the limiting case that the regional stress is zero, all stress changes are positive and large rotations occur far from the source, regardless of whether such slip directions are possible in that environment. For an infinitely large regional stress, no rotations of the optimal planes occur, and the areas of the positive and negative fields exactly balance. For realistic assumptions about the regional stress (e.g., that the regional stress is 1-10 times the earthquake stress drop), large rotations are restricted close to the fault rupture, where the earthquake stress change is significant relative to the regional stress. Positive optimally-oriented stress changes are seen along the fault in Fig. 3b where the fault slip exceeded 6 m (as seen in Fig. 1b), but such positive changes apply to planes which strike at high angle to the North Anatolia fault. Far from the 1939 rupture, rotation of the optimal planes is negligible. For an apparent coefficient of friction m' of 0.4 in this stress field, it is seen that right-lateral faults striking east-west, such as the North Anatolian, are optimally oriented (Figs. 2b and 3b). Coulomb stress changes on optimally oriented planes are also plotted for a decade of secular stress buildup in Fig. 2b. Here the rotations are negligible because the stress per decade, about 1.5 bars, is small relative to the 100-bar regional stress. A complete description of this method, and its dependence on friction and the regional stress, is given in King, et al. (1994) .

To sum, we use the optimally-oriented Coulomb stress changes to visualize stress transfer, because the patterns are simpler, and because they do not depend on knowledge of the faults surrounding the source. Such figures also show the correspondence between regions of calculated stress change and background seismicity or aftershocks (Figs. 4g and 5), because small shocks can occur on small faults, which could take any orientation consistent with the regional stress. But for calculations of triggering, time advance, and earthquake probability, we use the resolved stress changes as shown in Fig. 3a and as listed in the tables.

STRESS EVOLUTION DURING THE SEQUENCE

The buildup of stress at successive rupture sites, as well as the competition between secular stress accumulation and earthquake stress drop, are illustrated by sequential plots of the Coulomb stress change (Fig. 4). The stress increase along the North Anatolian fault, most evident outside the rupture zones (yellow), is a product of the secular fault slip at depth. Earthquakes generally relieve stress along the ruptures (purple zones), and typically transfer stress at some sites beyond the rupture tips and off the fault (red). Large earthquakes in 1939, 1943, and 1944 (Fig. 4a-d) profoundly decreased the stress over a distance of ~50 km normal to the fault; with time, this zone of diminished stress narrows. Compare, for example, the purple zone of the 1943 shock in Fig. 4c with the same region an half-century later in Fig. 4g. Moderate earthquakes in 1957 and 1967 (Fig. 4e-f) extended the earthquake sequence 100 km westward, but these shocks redistributed rather than diminished the stress within 50 km of the fault, and thus the western North Anatolian fault could re-rupture long before its central segments. The calculated stress reduction near the 1942 shock is likewise modest, suggesting that this section could also re-rupture. Though imperfect, the correlation between sites of calculated stress increase and seismicity (Fig. 4g) suggests that stress remains high at several sites along the North Anatolian fault, such as the Yedisu segment (km 450-500 in Fig. 4g).

The occurrence of a large earthquake off the North Anatolian fault in 1971 lends additional evidence for the stress-triggering hypothesis (Fig. 5). Of the four zones brought closer to failure after the 1949 shock, two sustained M>=6.7 earthquakes (beyond the end of the 1949 rupture in 1966, and in an off-fault lobe in 1971). A third site sustained an M=5.6 shock (in 1967) beyond the 1949 rupture at the east end of the Yedisu segment (Fig. 5b). The left-lateral East Anatolian fault ruptured 50 km south of where it joins the North Anatolian fault (Seymen & Aydin, 1972) . The preceding North Anatolian earthquakes increased stress on the East Anatolian fault by 0.6 bars, with the stress maxima centered on the future 1971 rupture zone. Note that stress resolved on the East Anatolian fault reaches its maxima near the future 1971 epicenter, and remains above 0.5 bars for most of the 1971 rupture zone (Fig. 5a). In addition, most fault segments that have not ruptured were brought farther from failure by the 1939-49 shocks (Fig. 5a). Finally, most small earthquakes occurred where the stress on optimally-oriented faults is calculated to have risen (Fig. 5b).

STRESS AT FUTURE RUPTURE SITES

Nine out of 10 shocks occurred where the mean stress over the entire future rupture had increased, typically by 2-4 bars (Table 2, col. 4). Similarly, 9 of 10 epicenters struck where the stress had been increased by the preceding earthquakes, typically by 3 bars (Table 2, col. 3). This calculation is independent of the regional or tectonic stress, and depends only on the fault slip, geometry, and the friction, m'. The stress transfer averages about 20% of the stress released by the earthquakes (Table 1, col. 7), a substantial trigger.

Although it is unknown whether the stress change along the future rupture, or at the future epicenter, is most important to triggering, the results for both assumptions are quite similar (Table 2). Faults are inherently complex, en echelon, and multi-stranded on many scales. Thus it is also unknown whether the stress change resolved on the fault plane as defined by its surface trace (as listed in the tables), or the stress change on optimally-oriented planes (as shown in Fig. 4) is most important to earthquake triggering. The optimally-oriented stress increases are about 25% larger than the resolved stress changes. Thus despite uncertainty in identifying the stress component that is most effective in triggering or advancing future earthquakes, the results lead to a consistent finding that the transfer of stress by one earthquake to another promoted the Anatolia sequence.

Scholz (1990) argued that the 1943 epicenter lies at the 'wrong' end of the 1943 rupture, because the epicenter locates at the end of the rupture farthest from the preceding 1942 shock. However, the calculated stress change at the end of the 1943 rupture closest to the 1942 shock inhibited failure (Fig. 3), and the 1943 epicenter lies within 40 km of where the stress change is most positive (Fig. 3a-b). Only the 1949 earthquake struck farther from the stress maxima associated with the preceding shocks (Fig. 2d), which is surprising because the intervening Yedisu segment last ruptured in 1784, and so the accumulated stress should have been high. Seismicity is now concentrated along this segment (Fig. 3g). The much better located aftershocks of the 1992 earthquake lie in regions of calculated failure stress increase (Nablant, et al., 1996) .

Most fault segments that sustained stress decreases have not ruptured, a further indication that stress changes influence earthquake occurrence. The typical stress change for the dozen unruptured segments since 1939 is -0.1 to -0.6 bars (Table 3, col. 2), in comparison with a 2- to 4-bar increase for those that have ruptured (Table 2, col. 3). Even when the secular stress accumulation during 1939-95 is included, the stress changes on the unruptured segments facilitated failure by only 1.2-1.6 bars (Table 3, col. 4), in comparison with a 3.6- to 6.1-bar increase for the segments that ruptured (Table 2, col. 5).

EARTHQUAKE PROBABILITIES

The effect of the stress change on times of earthquake recurrence can be cast as a change in the probability of future events. The times of future earthquakes along a fault segment are uncertain because of intrinsic variability of the earthquake faulting process and uncertainty of the observations used to estimate recurrence time. Estimations of the probability of future events over a given time interval provide the means to account for these uncertainties. Departing from previous studies, which consider only a permanent effect of stresses on segment probabilities (Cornell, et al., 1993; Working Group on California Earthquake Probabilities, 1990; Working Group on the Probabilities of Future Large Earthquakes in Southern California, 1992), we consider both permanent and transient effects of the stress changes on earthquake probabilities.

Segment Probability Prior to a Stress Step

Two models for estimation of earthquake probabilities are in general use, the stationary Poisson model and the conditional probability model (Cornell, 1968; Hagiwara, 1974). The conditional probability model can be tailored to find the effects elapsed time and stress changes on earthquake probabilities. We first present results from the simple Poisson model for comparative purposes and for later use in addressing transient effects of stress changes on probabilities. The stationary Poisson model, assumes the probability of an earthquake in a time interval is independent of the elapsed time from previous events. The probability of at least one event in the interval Dt is

,

(2)

where r is a constant occurrence rate for earthquakes that rupture the segment of interest and N is the expected number of such events in the interval Dt.

With the conditional probability model, probability can increase with time to represent increasing stress on a fault segment toward an uncertain stress threshold. We estimate the probability for recurrence of an earthquake on a fault segment prior to the stress step, given an elapsed time t from the previous earthquake, following the method of the Working Group on California Earthquake Probabilities (1990). The probability for recurrence of slip in any time interval (t, t+Dt) is

,

(3)

where f(t) is the probability density function for the uncertain recurrence time T for a segment rupturing earthquake. The probability, conditional on the earthquake not occurring prior to t, is

,

(4)

We assume a lognormal probability distribution of recurrence times

,

(5)

where m is the median and s is the standard deviation of the natural logarithm of the random recurrence time.

To estimate probabilities, we require values for m and s, as well as the time elapsed t during the 1939-67 sequence. Because the observations are sparse and uncertain, we do not distinguish different repeat times along the North Anatolian fault; instead we use the portions of the fault for which the record is longest to estimate a generic repeat time (Fig. 7). Although segment probabilities are sensitive to m, s and t, we show that probability gains associated with the stress steps (the ratios of probability after the steps to the probability before the steps) are insensitive to parameter choices. In the west (at about km = -200 in Fig. 7), earthquakes struck in A.D. 1035 , 1668, and 1944. For the central region, at km = -50, events occurred in A.D. 1050 , 1668, and 1943. For the eastern region near Erzincan at km = 350, earthquake took place in 1043 A.D., 1254, and 1939 (Ambraseys, 1970; Ikeda, et al., 1991; Ambraseys & Finkel, 1995). Together these yield m=450 yr, with s = 220 yr. The derived coefficient of variation of 0.5 is in accord with observations for faults with longer paleoseismic records, such as the southern San Andreas (Working Group on California Earthquake Probabilities, 1995). The time t elapsed between the 1939-67 sequence and the previous events in 1254-1668 is taken to be ~425 yr (a weighted average) in a 450± 220-year cycle. For the Poisson calculation (eq 2) the earthquake rate r is taken as 1/m. The stressing rate in our model is 0.15 bar yr-1 along most of the North Anatolian fault system (Fig. 2b).

The fault slip rate of 24 mm/yr, an average secular stressing rate of 0.15 bar/yr, and repeat time of 450 years, give a mean slip of 11 m per event and mean stress drop of 68 bars. During the twentieth century, the slip and stress drops are lower than this estimate except for the 1939 earthquake, suggesting that we may have overestimated the repeat time and thus underestimated the earthquake probability. This could arise if some large earthquakes are missing from the historical record. To examine the impact of overestimating the repeat time, and to define a range of probabilities appropriate to the observations, we also calculate probabilities a using an alternate set of parameters with repeat time. We arbitrarily halve the repeat time, leaving the coefficient of variation at 0.5. Thus m=225 yr, s=110 yr. For these calculations, for the elapsed time we use the time since the great 1668 earthquake (Fig. 7), so t=271 yr. The mean recurrence time of 225 years gives a mean event slip of 5.4 m per event and mean stress drop of 34 bars.

For the time interval used in this study, Dt=10 years, the first set of parameters (m=450 yr, s=220 yr, t=450 yr) give generic segment probabilities of 0.022 and 0.036 for the Poisson and conditional probability models, respectively, and the second set of parameters (m=225 yr, s=110 yr, t=271 yr) give generic segment probabilities of 0.044 and 0.130 for the Poisson and conditional probability models, respectively. Because the elapsed times are close to the mean recurrence times, the conditional probabilities are larger than the Poisson probabilities for both parameter sets.

Permanent effect of Stress Change

Increasing (or decreasing) the Coulomb stress on a fault segment permanently shortens (or lengthens) the time required for tectonic stressing to bring a segment to failure (Fig. 6a), and thus causes a permanent change in conditional probability. The conditional probability model can be adapted to estimate the effect of stress changes by equating a stress change with the time required to accumulate stress through secular stressing.

Two very similar methods have been proposed to estimate the effect of a stress increase on the conditional probability. The first method advances the elapsed time in the conditional probability calculation (eqs 3-5) from t to t' by the equivalent time required to accumulate the stress step Ds through the secular stressing process (Dieterich, 1988)

,

(6)

where is tectonic stressing rate. The second approach reduces the expected median recurrence time from m to m' by the equivalent time required to accumulate the stress step through the secular stressing process (Working Group on California Earthquake Probabilities, 1990)

,

,

(7)

Reducing m or increasing t for a positive step in stress increases the conditional probability of an earthquake (Fig. 6b, dotted to dashed lines). We have employed eq (7) in computing conditional probabilities following a stress step, because it is consistent with the concept that recurrence time is reduced by a step increase in stress. Both methods yield similar results, though eq (7) yields larger changes of probability for a given stress step. Segment probabilities following the stress step are given in Table 4 (col. 5) for the first parameter set, and in Table 5 (col. 5) for the second parameter set.

Transient effect of Stress Change

The existence of foreshocks and aftershocks demonstrate that when an earthquake occurs there is a large transient increase in the probability of additional earthquakes in the surrounding area. Similarly, global statistics of earthquake pairs reveal strong clustering in space and time, in which the occurrence of one earthquake increases the probability of a second earthquake, with the probability decaying with time and distance from the first event (Kagan and Jackson, 1991). These transient increases of earthquake probabilities are among the most prominent of statistical features of earthquake occurrence. A quantitative and unified explanation of aftershock distributions and decay, global clustering statistics, and foreshock statistics, is given by a single model in which the rate of earthquake occurrence is perturbed by the local stress increase caused by a prior earthquake (Dieterich, 1994; Dieterich & Kilgore, 1996). We employ this model to calculate this transient change of the segment earthquake probabilities.

The model is based on the constitutive formulation for rate of earthquake activity proposed by Dieterich (1994), derived from laboratory observations of rate- and state-dependent fault properties. Rate- and state-dependence of fault properties has been observed for a diverse variety of materials over the range of conditions for crustal earthquakes. Numerical simulations using these fault constitutive properties reproduce the full range of observed fault slip phenomena, including laboratory observations of spontaneous time-dependent nucleation of slip instabilities over a range of stresses above some minimum critical stress level, and healing following slip (Dieterich and Kilgore, 1996). A consequence of clustering statistics and time-dependent nucleation is that earthquake rates at all magnitudes undergo a strong transient amplification at the time of a step increase of stress, followed by 1/t decay to their background rate (Fig. 6b).

Because the transient effect of the stress change is expressed as a change in expected rate of segment events, it is convenient to formulate the probability analysis as a non-stationary Poisson process. Generalizing eq (2) gives

,

(8)

where, Pn is the net probability, which combines the transient and permanent effects of the stress change on earthquake probability and R(t) is now a non-constant (decaying) earthquake rate following a stress step. Dt is measured from the time of the stress step; we use 10 years for these computations. To evaluate eq (8), we obtain N, by integrating the solution for R(t) following a stress step (Dieterich, 1994; his eq 12). For the interval 0 to Dt, this yields

,

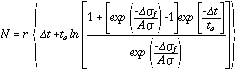(9)

where r is the permanent background component of the earthquake rate following the stress step (Fig. 6b), ta is the characteristic duration of the transient effect, and Dsf is the calculated Coulomb stress change. A is a dimensionless fault constitutive parameter and s is the effective normal stress. Since ta and As are unknown for the Anatolia sequence, we set ta = 10.2 yr, the value derived from pair clusters in the Harvard CMT global catalog for M>5 earthquakes at depths<70 km, and As=1 bar from analyses of aftershocks and foreshocks (Dieterich, 1994). Note that the transient effect disappears if Dsf = 0, that is N = r Dt.

In eq (9) r is the rate of activity implicit to the conditional probability following the stress step (Tables 4 and 5, col. 6). Hence, to evaluate r we equate the value of the conditional probability to a stationary Poisson probability and solve for r. From eq (2),

(10)

where, P is the previously obtained conditional probability for the fault segment following the stress step.

In summary, the net probability of events rupturing each fault segment (Tables 4 and 5, col. 7) combines both the permanent and transient effects of a stress step. Net probability is obtained by first computing the permanent effect of a stress change on the conditional probability using the approach of eq (7). Then the equivalent Poisson rate r for the permanent effect is obtained using eq (10) to evaluate eqs (8) and (9) for the net probability.

For completeness we noted that eq (9) assumes the background rate r after the stress step, is constant over the interval Dt, which it is not. Conditional probability grows slowly with elapsed time, requiring an increase of r with time (Fig. 6b). However, for the Anatolian computations the change of r over Dt=10 years is small relative to the magnitude of r, and the resulting error introduced by this approximation is slight. In cases where Dt is large relative to the repeat time T, and where higher accuracy in the application of eq (9) is sought, the time interval can be broken into n sub-intervals, . The conditional probabilities Pi, and expected number of events Ni are computed as before, for each sub-interval i. Pn for the entire interval is then given by

,

(11)

where Pn1 etc. are the net probabilities obtained for each sub-interval. Using the definition Pni=1-exp(Ni), eq (11) can be written as

,

(12)

where N=N1+N2+ .. Nn .

Net Probability Gain

The probability gain associated with the stress step is the net probability for some period after a stress increase, divided by the conditional probability prior to the step (Aki, 1981). The probability gains for the two sets of parameters are listed in Tables 4 and 5 (col. 8). Note that although net probabilities are very different for the two assumed repeat times, each set of recurrence parameters yields similar probability gains. It is also apparent that about 95% of the 10-yr gain is caused by the transient effect. In other words, both aftershocks and subsequent mainshocks are more likely in the stressed areas during the first decade after each large shock. We find an average three-fold gain in the probability of an M>=6.7 earthquake during the decade after each triggering event, with a wide range for individual triggers of 1-19.

LIMITATIONS OF THE ANALYSIS

Although we incorporate stress changes caused by earthquakes and secular fault slip, we make several assumptions that influence our results. Earthquake slip measured at the surface may under-represent the net slip at depth, and thus the stress change, by as much as 50%. Surface slip occasionally exceeds the slip at depth, as at the north end of the 1992 M=7.4 Landers, California, earthquake (Wald & Heaton, 1994) , so the calculated stress beyond the fault ends can also be too large. Our assumed 12.5-km depth of coseismic slip is consistent with the 1992 Erzincan earthquake (Barka & Eyidogan, 1993; Bennett, et al., 1996; Nablant, et al., 1996), but it is unknown for the preceding events. The deep slip rate used for the secular model is also uncertain by ±8 mm/yr (95% confidence) (Oral, 1994). In addition, we neglect two time-dependent effects: Pore-fluid flow could raise m' with time, as suggested by Harris & Simpson (1992), Jaumé & Sykes (1992), and Scholz (1990) , which would increase the stress changes by up to 25% (Table 2, col. 2). Postseismic asthenospheric relaxation also transfers stress to the upper crust. An 12.5-km-thick elastic plate overlying an inviscid fluid approximates complete relaxation of the lower crust; this yields stresses twice as high and twice as broad as those calculated here (Stein, et al., 1992). Thus most processes we omit would, if included, increase the calculated stress transfer and associated probability gains.

Several assumptions introduce uncertainty into our probability calculations. To estimate the permanent stress effects, we used a common repeat and elapsed time for large earthquakes on the Anatolian fault, whereas repeat times for the better studied San Andreas fault differ by nearly a factor of two between the northern and southern segments. For the transient probability effects, we relied upon global average values for the key parameters because we lacked local information for Anatolia. Based on analyses of earthquakes elsewhere, these parameters could differ by ±50%. Fortunately, the probability gains listed in Tables 4 and 5 (col. 8) are less sensitive to these assumptions than the probabilities, particularly during the first decade after each triggering earthquake when transient effects are large.

IMPLICATIONS FOR EARTHQUAKE FORECASTING

We identify several faults with an heightened probability of failure. The port city of Izmit is most vulnerable to an earthquake on the Sapanca fault (Fig. 4g). Stress increases of 1.3-2.5 bars are found for the Geyve and Sapanca faults, which pose the greatest threat to Istanbul, particularly if the faults ruptured from east to west. The Sapanca fault last ruptured in 1878. We calculate a 30-yr probability during 1996-2026 for M>=6.7 shocks on the Geyve and Sapanca fault segments to be 12%; this probability is higher by a factor of 1.07 than the rate before the these segments were stressed by the 1967 earthquake. The Yedisu (last rupture in 1784), Ovacik, and Göynük (last event in 1866) faults near Erzincan have been stressed toward failure by 1.7-9.2 bars. Erzincan, badly damaged during the 1939 and 1992 earthquakes, would be most affected if these faults ruptured toward the city (Fig. 4g). We calculate a 30-yr probability during 1996-2026 for M³6.7 shocks on the Yedisu segment to be 15%; this is a factor of 1.35 higher than the rate before the these segments were stressed by the 1992 Erzincan earthquake.

The Anatolian findings complement studies of the triggering of main shocks, aftershocks, and fault creep in California. The 1992 M=7.4 Landers earthquake was calculated to have increased the stress by 1.5-3.0 bars where the M=6.5 Big Bear shock struck 3.5 h after the Landers main shock, and 65% of the Landers M³1 aftershocks occurred where the stress rose by >0.3 bars (King, et al., 1994) . The Landers earthquake increased the stress 40 km away on the San Andreas fault by an estimated 2-6 bars (Harris & Simpson, 1992; Jaumé & Sykes, 1992; Stein, et al., 1992) , with ~150 mm slip needed to relieve the imposed stress (King, et al., 1994) . Subsequent GPS (Shen, et al., 1994) and continuous strain (Wyatt, et al., 1994) measurements indicate that deep slip on the San Andreas fault of 115±47 mm occurred where the stress was calculated to have risen, and slip of -39±33 mm where the stress was calculated to have dropped, in close accord with the calculation. Stress changes associated with several other California earthquakes influenced subsequent seismicity (Jaumé & Sykes, 1996; Harris & Simpson, 1996; Harris, et al., 1995; Simpson & Reasenberg, 1994; Stein, et al., 1994) . Together, these results attest that faults are sensitive to small but sustained stress changes transmitted over tens to hundreds of kilometers.

The North Anatolia fault has experienced several historical episodes of migrating earthquake sequences (Fig. 7). Large earthquakes progressed ~250 km eastward during 967, 1035, and 1050 A.D. (Ambraseys, 1970). A sequence ruptured perhaps 700 km of the fault during 1650±20 to 1668 (Ikeda, et al., 1991; Ambraseys & Finkel, 1995). We suggest that the propensity of the fault zone toward progressive failure is a product of its simple, straight geometry, which, as seen in Fig. 4, makes for efficient transfer of stress; its isolation from other faults, which minimizes stress transferred between the North Anatolian and competing faults; and its en echelon character (Wesnousky, 1988) , which tends to keep the entire fault from rupturing at once (Fig. 1c). By contrast, the San Andreas fault, which lacks an historical record of progressive shocks, produces larger earthquakes along its smoother trace, and generally lies close to other major faults, making the stress transfer more irregular and complex.

CONCLUSIONS

We find that earthquake-induced stress increases of several bars promoted the North Anatolia earthquake sequence, each shock raising the probability of future earthquakes at the site of the next to strike. Our analysis is least successful in explaining the occurrence of the 1943 earthquake and the absence of a Yedisu segment earthquake. Nor do we account for the time lag between individual triggers and ruptures, which varied from months to decades.

Our results suggest that earthquakes interact: When a large shocks occurs, it changes the conditions for failure in its vicinity, altering the probabilities for future events. In contrast, current approaches to earthquake hazard generally assume a stationary Poisson process where the past behavior of large faults is unknown, in which earthquakes are assumed to occur randomly over time on a fault. Where more information is available, the time-predictable model (Shimazaki & Nakata, 1980) is employed, in which the probability of an earthquake of specified size and location drops after the rupture but does not change elsewhere. Ward (1996) considered the permanent effects of stress transfer in a synthetic seismicity model for southern California, finding significant fault interactions, as we do here. Two seismic hazard analysis for the San Andreas system (Working Group on California Earthquake Probabilities, 1990; Working Group on the Probabilities of future large earthquakes in southern California, 1992) considered Coulomb stress changes, but only for the permanent effect associated with the most recent large earthquake in the region. In contrast, we find that the transient effect dominates during the first decade after the triggering event, contributing both to the production of aftershocks and to the higher likelihood of subsequent mainshocks. This result may help to explain a stress-triggering paradox in southern California: For small-moderate southern California earthquakes since 1932, the influence of Coulomb stress changes were discernible for <5 yr (Harris, et al., 1995) , but persisted for 50 yr following the great 1857 M=7.8 earthquake in the same region (Harris & Simpson, 1996) . The transient effect decays within 5-10 years for large and small shocks alike, but only large shocks substantially perturb the permanent probabilities, and so their influence persists long after the transient effect subsides.

Clustering of strong shocks is the outstanding feature of seismicity over historical (Kagan & Jackson, 1991) and paleoseismic (Wallace, 1987) time periods. Clustering implies that the prospect of a large earthquake rises after a large event. Stress transfer offers a physical explanation for earthquake clustering and migration: stress drops on the slipped fault but rises at other sites nearby, bringing faults in these regions closer to failure. Coulomb stress calculations thus capture the most salient feature of earthquake distributions, and gives insight as to where the next event is more likely to strike
.

ACKNOWLEDGMENTS.
We thank Nicholas Ambraseys, Christopher Scholz, John Vidale, Robert Simpson, and Steven Ward for reviews of the manuscript, Pierre Briole for initial assistance, and the Institut de Physique du Globe de Paris for a visiting professorship (R.S.).

FIGURES and TABLES

Fig. 1. (a) Active faults in Turkey (Barka, 1992; Saroglu & Kusçu, 1992; Sengor, et al., 1985), with the North Anatolian fault in bold. GPS observations establish a 24±4 mm/yr (1s confid.) deep slip rate on the North Anatolian fault and reveal that the right-lateral transform describes a small circle about a (33.4±0.5°E, 31.1±1.3°N) Anatolia-Eurasia rotation pole, which lies at the intersection of the dashed red lines (Oral, 1994) . (b) Cumulative right-lateral slip associated with M>=6.7 earthquakes (Barka, 1995; Barka & Eyidogan, 1993; Bennett, et al., 1996) ; the sequence ruptured from warm to cool colors. Slip in the 1949, 1966, and 1971 shocks is approximate, and the reverse-slip component for the Ezine and Kursunlu faults is not shown. (c) The region inscribed by the solid red line in a is projected relative to the Anatolia-Eurasia rotation pole, so that a transform fault would strike due east-west; the North Anatolian fault is seen to deviate less than 40 km from being a simple right-lateral transform.

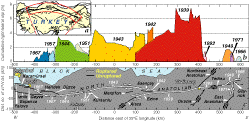
Fig. 2. Secular slip model used to calculate the loading of the North Anatolian fault system. (a) Steady deep slip below 12.5 km, as inferred from GPS observations (Le Pichon, et al., 1993; Oral, 1994; Oral, et al., 1997; Straub & Kahle, 1994; Straub, 1996) transfers stress to the seismogenic portion of the fault. The model shown, projected relative to the pole of rotation as in Fig. 1c, is used for the Coulomb stress changes on optimally oriented faults (Fig. 3. Fig. 4, and Fig. 5); an identical model projected in UTM coordinates, as in Fig. 1a, is used for the stress changes resolved on specific faults (Tables 1-3). (b) The secular stress rate is resolved on the fault at the indicated points, and also calculated for optimally oriented vertical strike-slip faults (color gradients). Deep slip and stress is distributed between two strands at the west end of the fault.

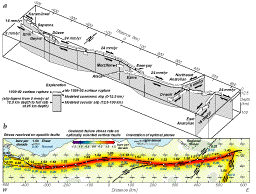
Fig. 3. Stress changes associated with the 1939 earthquake. (a) Coulomb stress change on major faults caused by the 1939 earthquake. Stress is resolved on the fault surface, projected in UTM coordinates, at a depth of 8 km. Faults are assumed to be vertical, except for the west end of the 1939 rupture, which dips 50° N. No information about the regional stress is needed for this calculation. The mean stress change along the future 1942 rupture is +1.4 bars. (b) Color gradients show the Coulomb stress change on optimally oriented vertical strike-slip faults at a depth of 8 km. The calculation assumes that the regional stress is 100 bars compression oriented 55° clockwise from the local Anatolian fault strike. Large rotations of the optimal planes are restricted close to the fault rupture, where the earthquake stress change is significant relative to the regional stress. Far from the 1939 rupture, rotation of the optimal planes is negligible.

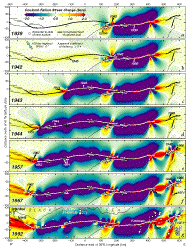
Fig. 4. Cumulative stress changes caused by large earthquakes and steady deep slip on the North Anatolian fault since 1939. In each panel, the epicenter of the next earthquake to rupture is circled. All but the 1943 epicenter lie in regions where the stress rose significantly, typically by 2-5 bars, owing to the foregoing shocks and deep fault slip. Relocated ISC earthquakes (Engdahl, et al., 1996) are shown in g, with the 1992 Erzincan aftershock sequence removed. Calculations are made in an elastic halfspace with a shear modulus of 3.15 x 1011 dyne-cm-2 and Poisson's ratio of 0.25. Earthquake slip is assigned as in Fig. 1b, assumed to be uniform over 0-12.5-km depth. The fault was digitized and stress was sampled at 5-km increments, and is projected as in Fig. 1c so that the regional stress maintains nearly a fixed angle to the fault.

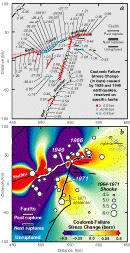
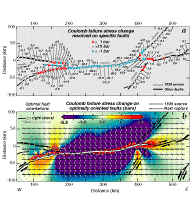
Fig. 5. Stress changes at the east end of the North Anatolian fault caused by 1939 and 1949 earthquakes (Ambraseys, 1988) . To emphasize the earthquake stress transfer, secular stress accumulation is not included in this plot; its inclusion would simply raise the stress along the North and East Anatolian faults by 1-1.4 bars. Projection as in Fig. 4. (a) The 1939 and 1949 earthquakes highly stress the sites of the future 1966 and 1971 earthquakes. Most segments that did not subsequently rupture were brought farther from failure except for the Yedisu segment. (b) Most aftershocks or small earthquakes occur in regions where the stress change on optimally-oriented strike slip faults was raised by the 1939-49 earthquakes. The optimal orientations for right- and left-lateral faults off the 1949 rupture zone is shown with the assumed regional stress direction, sr. Earthquakes from 1964 from Engdahl, et al. (1996) are shown, rather than from 1949, because of the poor network quality before 1964.

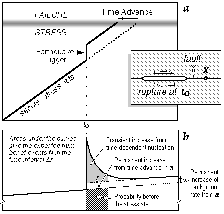
Fig. 6. Schematic illustration of a sudden stress increase Dsf on a fault at point x near an earthquake rupture at time to (inset). (a) The stress increase advances the time to the next rupture. If the stress were closer to failure at the time of the stress step, the trigger might have triggered an earthquake immediately. (b) The associated short-term (transient) and long-term (permanent) probability gain (Dieterich & Kilgore, 1996) . The transient gain (curved portion of solid line) scales with the rate of aftershock decay, and the permanent gain (dashed to solid line) is typically a factor of 1.12 higher than the probability before the triggers the Anatolian sequence.

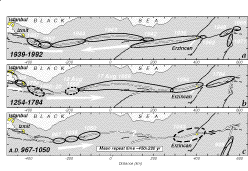
Fig. 7. Rupture zones for large historical earthquakes along the North and East Anatolian faults (Ambraseys & Finkel, 1988; Ambraseys & Finkel, 1995; Barka, 1992; Ikeda et al., 1991) . Zones for earthquakes before 1939 are based largely on isoseismals, and are thus approximate. Earthquake progressions, indicated by arrows, occurred during three sequences but in different directions and rates.

TABLE 1. Earthquake parameters and stress transfer
Earthquake		Moment mag. M	Mo (10 26 dyn-cm)**	Mean Dt* (bar)	Stress trigger‡ (bar)	Trigger ratio§ (%)	Time advance (yr)¶
Year	Date
1939	26 Dec	7.9	52.0	60	--	--	--
1942	20 Dec	6.9	1.7	42	4.7	11	8.4
1943	26 Nov	7.7	29.0	48	0.6	1	0.0
1944	01 Feb	7.5	15.0	34	5.8	17	31.4
1949	17 Aug	7.1	3.5	40	1.3	3	2.1
1951	13 Aug	6.8	1.4	25	1.7	7	11.0
1957	26 May	6.8	1.4	22	5.4	25	28.6
1966	19 Aug	6.6	0.6	15	8.2	55	30.0
1967	22 Jul	7.0	2.7	18	4.4	24	12.3
1971	22 May	6.8	1.2	11	3.5	32	4.6
1992	13 Mar	6.5	0.4	27	16.0	59	125.0
Average (all values)				31	5.2	24	25.3
Average (min/max excluded)				34	4.4	22	18.1
** Seismic moment calculated from surface slip (Fig. 1), assuming a 0 to 12.5-km width of faulting, and a shear modulus G of 3.15 x 1011 dyne-cm-2.
* Mean static shear stress drop of all 5-km-long rupture patches.
‡ Mean earthquake-induced plus secular stress change along future ruptures.
§ Stress trigger (col. 6) divided by succeeding earthquake stress drop (col. 5).
¶ Mean earthquake-induced stress change (for m=0.4) along the future rupture zone divided by the modeled secular stressing rate along that rupture.

Three modes to weigh the effect of the stress changes at the sites of future earthquakes. The trigger ratio is the Coulomb stress increase divided by the subsequent earthquake stress drop (col. 6/col. 5); the time advance gives the Coulomb stress increase divided by the local secular stressing rate.

TABLE 2. Stress transfer to future ruptures
	Coulomb failure stress change (bars)
	Earthquakes only			Earthq.+secular
Triggered Event	Epicentre m '= 0.75	Epicentre m ' = 0.4	Mean m ' = 0.4	Epicentre m ' = 0.4	Mean m ' = 0.4
1942	11.75	4.63	1.3	4.7	1.5
1943	0.00	0.01	-0.0	0.6	0.6
1944	6.56	6.39	4.8	7.3	5.6
1949	0.61	0.53	0.3	1.3	1.4
1951	1.49	1.71	1.7	1.7	1.7
1957	3.47	3.45	4.0	5.4	5.9
1966	3.85	4.03	3.0	8.2	5.4
1967	1.70	1.47	1.4	4.4	4.3
1971	0.71	0.58	0.5	3.5	3.2
1992	9.60	8.00	19.0	16.0	31.6
Average	4.0	3.1	3.7	5.2	6.1
min/max excluded	3.5	2.9	2.0	4.4	3.6

Cumulative stress transferred by M>=6.7 earthquakes and by secular stress accumulation since 1939, resolved onto future ruptures at 8 km depth. Faults were digitized at 5-km increments, with calculations performed with the fault projected in UTM coordinates, as in Fig. 1a. The stress change shown for the 1942 earthquake assumes that the Ezine fault (Fig. 1c) has a 50°-N dip and a 1:1 right-reverse-slip component (if the Ezine is treated as a vertical strike-slip fault, the mean change on the 1942 rupture zone is -6.0 bars and the epicentral change is -3.0 bars). The stress transferred by the 1951 earthquake is calculated for the 60°N-dipping Kursunlu thrust fault (Pinar, 1953) , although the epicenter could lie on the North Anatolian fault. The epicentral stress for m'=0.75 gives results for low pore fluid pressure.

TABLE 3. Stress on unruptured faults
	Coulomb stress change (bars)
	Earthquakes		Earthq.+secular
Fault	Max	Mean	Max	Mean
Yalova	0.03	0.02	1.3	1.3
Sapanca	0.5	0.2	1.6	1.3
Geyve	2.6	-1.6	6.7	2.5
Hendek	1.6	0.8	1.8	1.0
Düzce	2.3	-2.5	4.1	-0.7
Merzifon	-0.3	-1.4	0.4	-0.7
Alaca	3.0	0.2	3.0	0.2
Esençay	-3.7	-9.8	3.6	-2.5
Ovacik	8.0	1.8	7.6	1.7
NE Anat.	0.9	-0.3	0.1	-0.8
Yedisu	2.3	1.4	10.1	9.2
Göynük	5.4	3.5	8.1	6.2
Average	1.9	-0.6	4.0	1.6
min/max excluded	1.8	-0.1	3.8	1.2

Calculated stress transferred by M>=6.7 earthquakes and secular accumulation during 1939-95, for m'=0.4, resolved onto unruptured faults, listed from west to east (see Figs. 1c & 3g).

TABLE 4. Triggered earthquake probabilities (450±220 yr repeat time)
		Probability before the stress step		recurrence* time change (yr)	Conditional probability after the stress step‡		Probability gain (col. 7÷ col. 4)
Triggered Year	Shock Date	Poisson	Conditional †		Permanent effect	Transient + perm. effect
1942	20 Dec	0.022	0.036	-8.4	0.038	0.074	2.0
1943	26 Nov	0.022	0.036	0.0	0.036	0.036	1.0
1944	1 Feb	0.022	0.036	-31.4	0.041	0.204	5.6
1949	17 Aug	0.022	0.036	-2.1	0.037	0.044	1.2
1951	13 Aug	0.022	0.036	-11.0	0.038	0.087	2.4
1957	26 May	0.022	0.036	-28.6	0.041	0.174	4.8
1966	19 Aug	0.022	0.036	-30.0	0.041	0.140	3.9
1967	22 Jul	0.022	0.036	-12.3	0.038	0.078	2.1
1971	22 May	0.022	0.036	-4.6	0.037	0.050	1.4
1992	13 Mar	0.022	0.036	-125.0	0.059	0.704	19.4
Average				-25.3	0.041	0.159	4.9
Average (min/max values excluded)				-16.1	0.039	0.105	2.9

† Elapsed time is assumed to be 425 yr (weighted average time since complete rupture of the North Anatolian fault in earthquakes during 1254 and 1668; see Fig. 7).

* From eq (7), using the stress transfer in Table 2 (col. 4) divided by the secular stressing rate for each rupture zone (0.10-0.15 bar/yr) as shown in Fig. 2b.

‡ This uses the stress-modified recurrence time to compute the conditional probability for the ten years after the stress step.

TABLE 5. Triggered earthquake probabilities (225±110 yr repeat time)
		Probability before the stress step		recurrence* time change (yr)	Probability after the stress step‡		Probability gain (col. 7÷ col. 4)
Triggered Year	Shock Date	Poisson	Conditional †		Permanent effect	Transient + perm. effect
1942	20 Dec	0.043	0.130	-8.4	0.136	0.254	2.0
1943	26 Nov	0.043	0.130	0.0	0.130	0.130	1.0
1944	1 Feb	0.043	0.130	-31.4	0.155	0.599	4.6
1949	17 Aug	0.043	0.130	-2.1	0.131	0156	1.2
1951	13 Aug	0.043	0.130	-11.0	0.138	0.296	2.3
1957	26 May	0.043	0.130	-28.6	0.152	0.533	4.1
1966	19 Aug	0.043	0.130	-30.0	0.154	0.453	3.5
1967	22 Jul	0.043	0.130	-12.3	0.139	0.296	2.1
1971	22 May	0.043	0.130	-4.6	0.133	0.175	1.3
1992	13 Mar	0.043	0.130	-125.0	0.252	0.996	7.7
Average				-25.3	0.152	0.386	3.0
Average (min/max values excluded)				-16.1	0.142	0.342	2.6

† Elapsed time is assumed to be 271 yr (time since the great 1668 earthquake in Fig. 7).

* From eq (7), using the stress transfer in Table 2 (col. 4) divided by the secular stressing rate for each rupture zone (0.10-0.15 bar/yr) as shown in Fig. 2b.

‡ This uses the stress-modified recurrence time to compute the conditional probability for the ten years after the stress step.

REFERENCES

Aki, K., A probabilistic synthesis of precursory phenomena, In D. W. Simpson & P. G. Richards (Eds.), Earthquake Prediction - An International Review (pp. 566-574). Maurice Ewing Series 4, AGU, 1981.

Allen, C. R. (1969). Active faulting in northern Turkey, Contrib. 1577, 32 pp., Div. Geol. Sci., Calif. Inst. Technol.

Ambraseys, N. N., Some characteristic features of the Anatolian fault zone, Tectonophysics, 9, 143-165, 1970.

Ambraseys, N. N., Engineering seismology, Earthqu. Engin. and Structural Dynamics, 17, 1-142, 1988.

Ambraseys, N. N., and C. F. Finkel, The Anatolian earthquake of 17 August 1668, In W. H. K. Lee, H. Meyers, & K. Shimazaki (Eds.), Historical Seismograms and Earthquakes of the World (pp. 173-180). New York: Academic Press, 1988.

Ambraseys, N. N., and C. F. Finkel, The Seismicity of Turkey and Adjacent Areas: A historical review, 1500-1800. Istanbul: Muhittin Salih EREN, 1995.

Andrieux, J., S. Över, A. Poisson, and O. Bellier, The North Anatolian fault zone: distributed Neogene deformation in its northward convex part, Tectonophys., 243, 135-154, 1995.

Barka, A., Slip distribution along the rupture zones of the 1939-1967 large earthquake migration in the North Anatolian fault, Bull. Seismol. Soc. Am., in press, 1996.

Barka, A., and H. Eyidogan, The Erzincan earthquake of 13 March 1992 in eastern Turkey, Terra Nova, 5, 190-194, 1993.

Barka, A. A., The North Anatolian fault zone, Annales Tectonicae, VI suppl., 164-195, 1992.

Bennett, R., R. Reilinger, and A. Barka, Coseismic displacement of the 1992 Erzincan earthquake, Eastern Turkey, from GPS observations, in prep., 1996.

Cornell, C. A., S.-C. Wu, S. R. Winterstein, J. H. Dieterich, and R. W. Simpson, Seismic hazard induced by mechanically interactive fault segments, Bull. Seismol. Soc. Amer., 83, 436-449, 1993.

Dewey, J. W., Seismicity of northern Anatolia, Bull. Seismol. Soc. Amer., 66, 843-868, 1976.

Dieterich, J., A constitutive law for rate of earthquake production and its application to earthquake clustering, J. Geophys. Res., 99, 2601-2618, 1994.

Dieterich, J. H., Probability of earthquake recurrence with nonuniform stress rates and time-dependent failure, Pure and Applied Geophys., 126, 589-617, 1988.

Dieterich, J. H., and B. Kilgore, Implications of fault constitutive properties for earthquake prediction, Proc. Nat. Acad. Sci. USA, 93, 3787-3794, 1996.

Engdahl, E. R., R. D. Van der Hilst, and R. P. Buland, Global teleseismic earthquake location with improved travel times and procedures for depth determination, Bull. Seism. Soc. Am., in prep., 1996.

Gülen, L., A. Barka, and M. N. Toksöz, Kitalarin Çarpi_masi ve ‹lg›l› Kompleks deformasyon: Mara_ Üçlü Eklem› ve Çevre Yapilari, Yerbilimleri (Bull. Earth Sci. Applica. and Res. Centre Hacettepe Univ.), 14, 319-336, 1987.

Harris, R. A., and R. W. Simpson, Changes in static stress on southern California faults after the 1992 Landers earthquake, Nature, 360, 251-254, 1992.

Harris, R. A., and R. W. Simpson, In the shadow of 1857-Effect of the great Ft. Tejon earthquake on subsequent earthquakes in southern California, Geophys. Res. Letts., 23, 229-232, 1996.

Harris, R. A., R. W. Simpson, and P. A. Reasenberg, Influence of static stress changes on earthquake locations in southern California, Nature, 375, 221-224, 1995.

Ikeda, Y., Y. Suzuki, E. Herece, F. Saroglu, A. M. Isikara, and Y. Honkura, Geological evidence for the last two faulting events on the North Anatolian fault zone in the Mudurnu Valley, western Turkey, Tectonophysics, 193, 335-345, 1991.

Jackson, J., and D. McKenzie, The relationship between plate motions and seismic moment tensors, and the rates of active deformation in the Mediterranean and Middle East, Geophys. J. Int., 93, 45-73, 1988.

Jaumé, S. C., and L. R. Sykes, Change in the state of stress on the southern San Andreas fault resulting from the California earthquake sequence of April to June 1992, Science, 258, 1325-1328, 1992.

Jaumé, S. C., and L. R. Sykes, Evolution of moderate seismicity in the San Francisco Bay region, 1850 to 1993: Seismicity changes related to the occurrence of large and great earthquakes, J. Geophys. Res., 101, 765-789, 1996.

Kagan, Y. Y., and D. D. Jackson, Long-term earthquake clustering, Geophys. J. Int., 104, 117-133, 1991.

Kasahara, K., Earthquake Mechanics. Cambridge: Cambridge Univ. Press, 1981.

Kasapogu, K. E., and M. N. Toksöz, Tectonic consequences of the collision of the Arabian and Eurasian plates: Finite element models, Tectonophysics, 100, 71-95, 1983.

Ketin, I., Uber die nordanatolische Horizontalverschiebung, Bull. Min. Res. Explor. Inst. Turkey, 72, 1-28, 1969.

King, G. C. P., R. S. Stein, and J. Lin, Static stress changes and the triggering of earthquakes, Bull. Seismol. Soc. Amer., 84, 935-953, 1994.

Le Pichon, X., N. Chamot-Rooke, P. Huchon, and P. Luxey, Implications des nouvelles mesures de géodésie spatiale en Grèce et en Turquie sur l'extrusion latérale de l'Anatolie et de l'Egée, C. R. Acad. Sci. Paris, t. 316, Série II, 983-990, 1993.

Mogi, K., Earthquake Prediction. Tokyo: Academic Press, 1985.

Nablant, S. S., A. A. Barka, and Ö. Alptekin, Failure stress change caused by the 1992 Erzincan earthquake (Ms=6.8), Geophys. Res. Letts., 23, 1561-1564, 1996.

Neugebauer, J., Structures and kinematics of the North Anatolian fault zone, Adapazari-Bolu region, northwest Turkey, Tectonophys., 243, 119-134, 1995.

Oral, M. B. (1994) Global Positioning System (GPS) Measurements in Turkey (1988-1992): Kinematics of the Africa-Arabia-Eurasia Plate Collision Zone,. Ph.D. thesis, 344 pp., Mass. Inst. Tech.

Oral, M. B., R. E. Reilinger, M. N. Taksöz, R. W. King, A. A. Barka, I. Kinik, and O. Lenk, Global Positioning System (GPS) measurements in Turkey (1988-1992): Kinematics of the Africa-Arabia-Eurasia Plate Collision Zone, J. Geophys. Res., submitted, 1997.

Pinar, N., Etude géologique et macrosismique du tremblement de terre de Kursunlu (Anatolie septentrionale) du 13 aout 1951, Rev. Fac. Sci. Univ. Istanbul, Series A, 18, 131-141, 1953.

Richter, C. F., Elementary Seismology. San Francisco: W.H. Freeman & Co., 1958.

Roeloffs, E. A., Fault stability changes induced beneath a reservoir with cyclic variations in water level, J. Geophys. Res., 93, 2107-2124, 1988.

Roth, F., Modelling of stress patterns along the western part of the North Anatolian fault zone, Tectonophysics, 152, 215-226, 1988.

Saroglu, F., and I. Kusçu, Active Fault Map of Turkey (1:1,000,000), In Ankara: Gen. Dir. of Mineral Res. & Explor. (MTA).

Scholz, C. H., The Mechanics of Earthquakes and Faulting. Cambridge: Cambridge University Press, 1990.

Sengor, A. M. C., N. Gorur, and F. Saroglu, Strike-slip faulting and related basin formation in zones of tectonic escape: Turkey as a case study, In K. T. Biddke & N. Christie-Blick (Eds.), Strike-slip Faulting and Basin Formation (pp. 227-264). Soc. Econ. Paleont. Min. Spec. Publ., 1985.

Seymen, I., and A. Aydin, The Bingöl earthquake fault and its relation to the North Anatolian fault zone, Bull. Miner. Res. Explor. Inst. Turkey, 79, 1-8, 1972.

Shen, Z.-K., D. D. Jackson, Y. Feng, M. Cline, M. Kim, P. Fang, and Y. Bock, Postseismic deformation following the Landers earthquake, California, 28 June 1992, Bull. Seismol. Soc. Amer., 84, 780-791, 1994.

Shimazaki, K., and T. Nakata, Time-predictable recurrence model for large earthquakes, Geophys. Res. Lett., 7, 279-282, 1980.

Simpson, R. W., and P. A. Reasenberg, Earthquake-induced static stress changes on central California faults, In R. W. Simpson (Eds.), The Loma Prieta, California, earthquake of October 17, 1989-Tectonic processes and models: U.S. Geological Survey Professional Paper 1550-F, 1994.

Stein, R. S., G. C. P. King, and J. Lin, Change in failure stress on the southern San Andreas fault system caused by the 1992 Magnitude=7.4 Landers earthquake, Science, 258, 1328-1332, 1992.

Stein, R. S., G. C. P. King, and J. Lin, Stress triggering of the 1994 M=6.7 Northridge, California, earthquake by its predecessors, Science, 265, 1432-1435, 1994.

Straub, C., and H.-G. Kahle, Global Positioning System (GPS) estimates of crustal deformation in the Marmara Sea region, Northwestern Anatolia, Earth & Planet. Sci. Letts., 121, 495-502, 1994.

Straub, C., Recent crustal deformation and strain accumulation in the Marmara Sea region, N.W. Anatolia, inferred from GPS measurements. Ph.D., Swiss Fed. Inst. of Technol. , 123 p., 1996.

Suzanne, P., N. Lyberis, J. Chorowicz, M. Nurlu, T. Yurur, and E. Kasapoglu, La géométrie de la faille anatolienne à partir d'images Landsat-MSS, Bull. Soc. géol. France, 8, VI, 589-599, 1990.

Wald, D. J., and T. H. Heaton, Spatial and temporal distribution of slip for the 1992 Landers, California earthquake, Bull. Seismol. Soc. Amer., 84, 668-691, 1994.

Wallace, R. E., Grouping and migration of surface faulting and variations in slip rates on faults in the Great Basin province, Bull. Seismol. Soc. Amer., 77, 868-876, 1987.

Ward, S. N., A synthetic seismicity model for southern California: Cycles, Probabilities, Hazard, J. Geophys. Res., in press, 1996.

Wesnousky, S., Seismological and structural evolution of strike-slip faults, Nature, 335, 340-342, 1988.

Working Group on California Earthquake Probabilities, Probabilities of large earthquakes in the San Francisco Bay region, California, U.S. Geol. Surv. Circular 1053, 1990.

Working Group on California Earthquake Probabilities, Seismic hazards in southern California: Probable earthquakes, 1994-2014, Bull. Seismol. Soc. Amer., 85, 379-439, 1995.

Working Group on the Probabilities of future large earthquakes in southern California (1992). Future Seismic Hazards in Southern California, Phase I: Implications of the 1992 Landers Earthquake Sequence, 42 pages). Calif. Div. Mines & Geol.

Wyatt, F., D. C. Agnew, and M. Gladwin, Continuous measurements of crustal deformation for the 1992 Landers earthquake sequence, Bull. Seismol. Soc. Amer., 84, 768-779, 1994.

Zoback, M. D., et al., New evidence on the state of stress of the San Andreas fault system, Science, 238, 1105-1111, 1987.