UDC: 69.02 Keywords: Design performance,
Multiple criteria
Comparative Performance Appraisal By Multiple
Criteria
For Design Alternatives
M.
Aygün
Associate Professor,
Department of Architecture,
An
analytical comparative method is proposed for the evaluation of relative
performance of design alternatives by multiple criteria which are expressed in
terms of quantitative design variables. Any one of the latter may be included
in one or more of the criterion functions. For each criterion the appropriate
performance function is applied to
the absolute values, which are then converted to weighted relative values.
Subsequently multiple statistical parameters are employed, also accounting for
the deviation of individual criterion performances. Finally, those alternatives
with above-average values for all statistical criteria can be rank-ordered. The
effect can be investigated of design variables on the overall performance of
each alternative. The method also allows the performances to be ascertained of
alternatives at each phase or over the complete life cycle and of phases in the
life cycle for the given set of alternatives.
Introduction
Common models of design processes
involve the configuration of a system invariably with many qualitative and quantitative
attributes, for each of which a design decision is required. Therefore, the
designer is confronted with the task of exploring the consequences of various
variable values and simultaneously resolving any conflicts between the
performance criteria for striking a balance between the attributes. An
analytical approach is deemed conducive to selecting the most satisfactory
solution, i.e. the primus inter pares,
since 'trial and error' approaches for alternative generation and evaluation
are obviously inefficient, leading to considerable abortive work, and are
liable to omit otherwise viable alternatives
The set of required criteria values
for a system design represents the user requirements or performance
specification also known as the demand profile which is attempted to match as
much as possible with the supply profile of the design proposals in accordance
with the raison d’etre of this
work. If the latter profile exceeds the former on some or all aspects then
overperformance due to overspecification of that proposal occurs. Conversely,
if the supply fails to meet the demand then underperformance arises because of
underspecification. While overperformance implies an excessive (surplus)
capacity and possibly cost-ineffectiveness, underperformance implies inadequacy
of the proposals.
Related works include that by
Müller who focuses on building elements and divides their main functions
into sub-functions, compares the performances of component alternatives and
then configures the element [ 1 ]. Reddy and
Mistry develop the modeling of uncertainty in selection of alternatives using
exact interval arithmetic whereby criterion values with upper and lower limits
of deviation are accounted for [ 2 ]. Iyengar,
et.al. introduce the concept of connectors to represent the interaction between
adjacent components and to provide for function sharing [ 3 ]. Sims and
Becker compare the demand profile of user requirements with the supply profiles
of building design alternatives and prescribe the best-match performance
concept for selection rather then
the maximum, average best or stereotype performance concepts [ 4 ]. Boubekri et
al. introduce neural networks as an analysis and evaluation method for design
problems with many possible configurations involving large number of
independent design variables [ 5 ]. D'Kruz and Radford present a method for
obtaining viable design alternatives through Pareto optimal dynamic
programming. Criteria are processed in sequence thereby progressively narrowing
down the range of viable solutions [ 6 ]. Cross
reviews the morphological chart method for generating alternatives and the
weighted objectives tree method for the evaluation [ 7 ]. Ullman
explicates product generation through concurrent design and discusses
performance evaluation through minimizing variation of critical parameters [ 8 ]. Coyle
describes grammar systems by which design generation can operate. Control of
these are achieved by various planning models, which also serve to resolve
goals in conflict [ 9 ]. Hatush and Skitmore
describe an additive model of the utility theory for multicriteria decision
analysis through utility functions in order to select the most suitable
contractor [ 10 ].
The fundamental elements idiosyncratic
of most evaluation methods are design variables, criteria and utility functions
as their genius loci. These elements
are reviewed below prior to applying them to the comparative appraisal of
alternatives in an a priori approach
described in this work.
Design Variables
Any quantifiable system is defined by
a set of constants and independent variables as design parameters. Various
performance criteria constitute the dependent variables of such a system.
Independent variables are categorized here by means of 5 binary descriptions as
follows:
1.Exogenous/ Endogenous: Variables
of the former type are restricted or dictated by an external or internal
constraint and are prescriptive, stipulated by user and mandatory requirements,
such as standards, regulations and codes, or by resources available at that
time. The restrictions on variables are in the form of specified discrete
values or permissible upper and lower limits, i.e, maximum and minimum.
Conversely, endogenous variables are at the discretion of the designer for
manipulation. Values assigned to these parameters are either empirical ,based
on personal or collective experiential knowledge, or even arbitrary for
purposes of intuitive exploration. However, in actual fact, designers rarely,
if ever, exercise complete control over any variable because of circumstantial
constraints in practice. Consequently, all endogenous variables can be regarded
as semi-exogenous.
2.Mono-dependent /
Multi-dependent: Variables of the latter type occur in more than one
performance function.
Mono-dependent variables, contrary to the previous, occur in only one function
and has no influence on any other.
3.Complimentary/
Contradictory: A variable is
either complimentary to any performance criterion or contradictory, describing
whether the variable has a positive or negative effect on performance as an
indication of the rise or fall in that criterion provided that all other
parameter values remain constant, i.e. whether the trend is directly or
inversely proportional. If the same variable is complementary to some criteria
while concurrently being contradictory to others then a conflict situation
arises. In that case a compromised value is required through optimization.
4.Coherent/ Incoherent: Any
variable influencing all relevant criteria in the same manner, i.e. positively
or negatively, are described here as coherent and those with diverse effects as
incoherent. Coherence is associated with a maximization or minimization process
and incoherence with optimization.
5.Qualitative/Quantitative: The 4
familiar types of measurement scales are nominal, ordinal, interval and ratio.
The first two involve qualitative and the last two quantitative values. The
work undertaken here is concerned primarily with quantity.The ensuing method is
directly applicable to interval and ratio scales while a conversion process is
required for the ordinal values which involve some subjective judgement.
Variables may be expressed as quality or quantity. The values ascribed to
qualitative variables are in the measurement scales of nominal or ordinal, , on
which arithmetic operations cannot be performed, whereas quantitative values
are in interval or ratio scales which involve quantities (e.g. kN, W) as well
as ratios (e.g. kN/kN, W/W) and coefficients (e.g.kN/m2, W/m2).
Physical Criteria
These are means of asserting
requirements on a particular aspect of design for quantitative evaluation,
preferrably as numerical expressions, which are most amenable to objective
manipulation. They are the dependent
variables of a system as expressed in terms of independent variables and
present the objective functions. As
mentioned earlier each criterion per se
includes one or more variables and similarly each variable can be a term in one
or more criterion functions. For each criterion a corresponding performance
function is required in order to establish the type of relationship between the
criterion and performance as described later. In the hypothetical set of 3
criterion functions (c) given below there are 5 variables (v).
c1=v1v3/v2 c2=v3v4 c3=v2
/v4v5
In case there is only one performance
value for each variable value, an interaction matrix as the example below, can
be used to explore the effects of variables on all criteria and consequently to
determine the presence of any coherent variables (Table 1). The plus or minus
sign in the matrix denotes the coherence or incoherence. Zero signifies that
there is no interaction between that variable and criterion. If all signs
ascribed to a column of this matrix are equal, i.e. plus or minus ignoring zero
which bears no effect, then that variable is deemed as coherent. In the example
given below v1 , v3
and v5 are coherent while v2 and v4 are
incoherent. Depending on whether the former are complementary or contradictory
to criteria they are assigned the maximum (v1, v3)or the
minimum (v5)variable value value respectively and regarded as
constants throughout the evaluation. They can hence be excluded from the
process of exhaustive enumeration for reducing the number of alternatives to be
generated for evaluation. Zero sign bears no effect. Conversely, if there are
opposite signs in any one column (i.e. v2 and v4) then an optimization
process is applicable to those criteria involved (c1, c2,
c3) for obtaining an compromised value of this variable.
Table 1
Interaction of Criteria (c) and Variables
(v)
|
|
v1 |
v2 |
v3 |
v4 |
v5 |
|
c1 |
+ |
- |
+ |
0 |
0 |
|
c2 |
0 |
0 |
+ |
+ |
0 |
|
c3 |
0 |
+ |
0 |
- |
- |
The acceptable limits of criteria are
stated in one of the following
formats: 1.Single limit (upper or lower), i.e. threshold (real or
integer numbers), 2.Two limits (upper and lower), i.e. range between upper and
lower limits, 2.1.Continuous (real numbers only), 2.2.Discrete (real or integer
numbers), 2.2.1.Regular progression, 2.2.1.1.Equal intervals (arithmetic
series), 2.2.1.2.Unequal intervals (geometric series), 2.2.2.Irregular
progression. The criteria yield values through performance statements
incorporating functions (expressions) and relational operators (<, £, >, ³) in
conjunction with logical operators (and, or, xor, etc.) as sentential
connectives.
Utility Functions
For each criterion a suitable type of
utility function needs to be selected. A 3-stage binary decision sequence can
guide the selection process of primary function types. These transitive
decision stages are explained as follows.
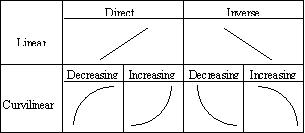
1. Direct or Inverse: Utility
is proportional to these values in the direct case and inversely proportional
in the inverse.
2. Linear or Curvilinear: The
anticipated rate of utility change determines whether the function is linear or
curvilinear.
3. Increasing or Decreasing: Curvilinear
functions display a trend of either increasing or decreasing rate of change
which is more for the lower parameter value range than the higher if this trend
is decreasing. The reverse holds true for the increasing trend. Furthermore the
intermediate range between the extreme utility values, i.e. minimum and
maximum, are higher for the decreasing trend than the increasing in direct
functions and visa versa in inverse.
6 primary types of utility functions
emerge from combination as illustrated by graphs of lines and curves in Table
2. They may be employed for deriving more complex types, such as
‘U’ and ‘S’ curves may be generated either by combining
the primary types with each other as required.
|
Table 2 Graphs of Primary Utility Functions |
Physical Evaluation
Initially physical criteria are
expressed as functions of variables and then absolute values of these criteria
functions are obtained for each generic laissez-faire
design alternative which is then tested for compliance with the permissible
values of performance criteria. The latter are either self-imposed by designer
or mandatory stipulated by legislation, such as building regulations, codes and
standards. Consequently some alternatives are pre-eliminated. As a second
option, only those alternatives with above-average values for any one of the
criteria are selected as prospective bona
fide solutions, reducing the total number of eligible alternatives further
for subsequent appraisal.
Corresponding absolute utility values
are calculated through the appropriate utility function. Since criteria can
have different dimensions, these values must be put in a non-dimensional form,
i.e.standardized, for the purpose of comparing performances of alternatives as
well as individual criteria. Therefore these values are converted from absolute
to relative by interpolation between the maximum and minimum absolute utility
values for each criterion, providing the deus
ex maschina.
Even though not recommended due to
their phenomenological implications, weighting factors may subsequently be
applied with reservation to the relative utility values for taking into account
the relative importance of each criterion. For ascertaining the weighting of
criteria, the design objectives can first be rank-ordered by paired comparisons
in a square matrix. Then, if there are more than one level of sub-objectives,
then an objectives tree can be drawn. This process enables to be determined the
weights relative to each other at the same branch level and consequently those
relative to the overall objective.
Statistical Evaluation
The previous relative physical
performance values are first normalized for manipulation. This procedure is the
same as that of the preceeding normalisation except that statistical criteria
are substituted in lieu of physical
criteria. Multiple statistical criteria are used here simultaneously as
criteriaof overall performance to enhance the conventional aggregation process.
The average value is thus augmented by the parameters of standard deviation and
coefficient of variation. Thus the distribution of the criteria values for each
alternative is accounted for. Other supplementary parameters may be included as
required, such as kurtosis and skewness. The values of these are ascertained
for each alternative. Corresponding absolute values are then obtained through
the appropriate function Finally, values are converted from absolute to
relative for each criteria as explained previously. The mean of these values
yield a single overall performance criterion for each entity under
consideration.
Method Outline
The proposed method comprises two
consecutive parts called Physical and Statistical Evaluation as clarified
above. They employ the same procedure but physical and statistical criteria are
substituted respectively. Each step is explained below in brief. Those
involving input may run concurrently.
Physical
Evaluation:
1. Physical
Criterion Functions (Input): Express the relevant physical criteria as
functions of independent design variables for achieving the preset objectives.
2. Physical
Utility Functions (Input): Establish the appropriate physical utility function
for each performance criterion in terms of that criterion.
3. Physical
Criterion Weights (Input): Rank-order and draw hierarchical tree for objectives
in order to set the relative weights of the corresponding physical criteria
with respect to their contribution
to achieve the objectives.
4. Physical
Criterion Values: Calculate the physical criterion values through that function
for each alternative.
5. Eligible
Alternatives (Elimination of Alternatives): Identify those alternatives which
satisfy all mandatory limits of physical criteria or which attain above-average
values for all criteria.
6. Absolute
Physical Performance Values: Calculate the absolute physical performance values
through that functions of each criterion for the alternatives.
7 Relative
Physical Utility Values: Standardize physical performance values by converting
them from absolute to relative through linear interpolation and apply the
weights if deemed appropriate.
Statistical
Evaluation:
1. Statistical
Criterion Functions (Input): Select the suitable statistical criterion
functions.
2. Statistical
Criterion Values: Calculate the statistical criterion values for each
alternative.
3. Absolute
Statistical Performance Values: Calculate the absolute statistical performance
values through that function of each criterion for the alternatives.
4. Relative
Statistical Utility Values: Convert statistical performance values from
absolute to relative through linear interpolation, thus non-dimensionalising
them.
5. Ranked
Shortlist: Prepare a ranked shortlist of satisfactory alternatives which have
attained above-average values for all statistical criteria.
For any system to be
regarded as satisfactory all statistical criteria must be above their
respective average values. Such a system is here deemed as well synthesized for
the intended purposes. Those fulfilling this prerequisite are then rank-ordered
according to their overall performance score, expressed by the relative
statistical utility average.
Life Cycle Analysis
Multiple criteria are especially
pertinent to life cycle analysis where various criteria are involved in
consecutive phases, e.g. on the subject of building elements: manufacture,
assembly, operation, refurbishment, disposal. At least one or more criteria are
applicable to any one of these phases. Furthermore, some criteria may apply to
any
number or all of the
phases, e.g. energy, ecology. Some pertain to a particular phase, e.g. user
comfort in the operation phase.
The performance of design alternatives
or phases relative to each other can be investigated based on aggregation of
criteria values over the domains.
This modus operandi therefore
allows the inter- and intra domain effects of the alternative attributes to be
explored. The procedure is accomplished in three consecutive stages.
Stage 1: The actual criteria values
are ascertained for each alternative included at each life cycle phase. Subsequently since the criteria mostly
have different dimensions, these values are standardized prior to converting
them to weighted utility values.
Stage 2: The previous values are
aggregated to obtain a single indicator for each phase of all alternatives and
presented in tabular form.
Stage 3: The overall utility values of
alternatives and/or phases can be determined and rank-ordered as a result of
row and/or column aggregation of the values obtained in penultimate stage.
Application
The proposed method is illustrated by
means of two worked examples of different applications.
First Example
A demonstrative exercise is undertaken
in the evaluation of the geometric efficiency of alternative rectangular
building forms. In the context of this exercise the relevant criteria are taken
as: 1.Earthquake resistance, 2.Energy conservation and 3. Land utilization.
These are then expressed as 5 separate functions of design variables. Some of
the criteria involve a reference cube of volume equal to that of the building
in question.
1.1. The long side
dimension (b) of a building must be small relative to the short side dimension
(a) on grounds of stability against earthquake along either one of the
orthogonal horizontal axes (b/a).
1.2. In addition, the
short side dimension (a) must be large compared to the building height (h) in
order to restrict sway and lateral shift of the centre of gravity (a/h).
2.1. For energy
efficiency a large volume (V) must be enclosed by a relatively small area of
external surface (Asb) where fabric heat loss occurs. This criterion
is expressed here as the ratio of the surface area of the reference cube (Asc=6V2/3)
to the area of the external surface of the block (Asb).
2.2. Since edges of a
building act as potential cold bridges, instigating interstitial or surface
condensation beside heat loss, the total edge length (Lb) is
required to be small compared to the surface area of the external envelope (Asb)
to avoid this mode of failure. This criterion is expressed here by the ratio of
the edge length of the reference cube (Lc=12V1/3) to the
edge length of the building (Lb).
3.0. Under
consideration of efficient land utilisation, the volume of enclosed space (V)
may be large compared to the ground area occupied by the building (Agb).
This criterion is expressed here by the ratio of the ground area of the
reference cube (Agc=V1/3) to the ground area of the
building (Agb).
The design process of
buildings may involve the following variables listed in conjunction with the
discrete values applicable to this example:
Design Variable Variable
Values
Total floor area (Atf) :1000 1100 1200
Number of storeys (ns) :1 2 3
Height of storey (hs) :3.0 3.3 3.6
Ratio of side dimensions (b/a) :1.0 1.5 2.0
The variable are confined to 3 values
each and the building form to rectangular blocks. The interactions between
design variables and physical criteria are tabulated below in Table 3. As
construed from this table all variables are incoherent, i.e. contain different
signs in any one column, therefore none of them can be eliminated from the
process of alternative generation.
Table 3
Interactions between Design Variables and
Criteria
|
Criteria |
Atf |
ns |
hs |
b/a |
|
b/a |
- |
+ |
0 |
+ |
|
a/h |
+ |
- |
- |
- |
|
Asc/Asb |
+ |
- |
+ |
- |
|
Lc/Lb |
+ |
- |
+ |
- |
|
Agc/Agb |
+ |
+ |
+ |
- |
The utility functions are specified as
linear and the weights as equal for both physical and statistical criteria. All
variable values are assumed as being compatible with each other. By means of
the available variable values for design variables 81 alternatives of building
form can be generated by combination. The physical criterion values are
calculated for each building form alternative. Those with below-average values
for any one of the criteria are eliminated from further evaluation. The
relative physical utility values are calculated by means of the corresponding
functions. This procedure is repeated for converting statistical criterion
values to the relative statistical utility values. In the final stage 11
alternatives have been identified as satisfying the requirement that all
statistical criteria attain above average values. Their design attributes
(variable values) and the corresponding relative statistical utility values are
presented in Table 4 below. As construed from this table B70 scores the highest
in terms of the average and the total,
B71 in terms of the coefficient of variation, B44 in terms of the
standard deviation.
Table 4
The Values of Relative
Statistical Utility (%) for
Shortlisted Alternatives and their
Attributes
|
Rank |
Design |
Statistical
Performance (%) |
Design Variables |
||||||
|
No. |
Alternatives |
Ave |
Dev |
Var |
Total |
Atf |
ns |
hs |
b/a |
|
1 |
A70 |
41.49 |
16.13 |
20.56 |
78.2 |
1200.0 |
2.0 |
3.6 |
1.0 |
|
2 |
A67 |
37.83 |
16.66 |
20.28 |
74.8 |
1200.0 |
2.0 |
3.3 |
1.0 |
|
3 |
A43 |
38.84 |
15.62 |
19.67 |
74.1 |
1100.0 |
2.0 |
3.6 |
1.0 |
|
4 |
A71 |
30.15 |
20.54 |
22.06 |
72.7 |
1200.0 |
2.0 |
3.6 |
1.5 |
|
5 |
A64 |
34.09 |
16.74 |
19.57 |
70.4 |
1200.0 |
2.0 |
3.0 |
1.0 |
|
6 |
A40 |
35.14 |
15.95 |
19.14 |
70.2 |
1100.0 |
2.0 |
3.3 |
1.0 |
|
7 |
A44 |
27.54 |
20.75 |
21.73 |
70.0 |
1100.0 |
2.0 |
3.6 |
1.5 |
|
8 |
A16 |
35.88 |
14.71 |
18.30 |
68.9 |
1000.0 |
2.0 |
3.6 |
1.0 |
|
9 |
A37 |
31.35 |
15.83 |
18.14 |
65.3 |
1100.0 |
2.0 |
3.0 |
1.0 |
|
10 |
A13 |
32.14 |
14.79 |
17.44 |
64.4 |
1000.0 |
2.0 |
3.3 |
1.0 |
|
11 |
A74 |
29.34 |
14.02 |
15.95 |
59.3 |
1200.0 |
3.0 |
3.0 |
1.5 |
Second
Example
The next worked example involves an
implementation on a set of 27 generic alternatives of an hypothetical
functional building element with 4 performance criteria at each life cycle
phase. The latter are functions of
physical or chemical attributes.
The assumed element under consideration is intended to act
simultaneously as a barrier and filter between the external and internal
environments by regulating mass and energy flows as with all other external
building elements. The alternatives are evaluated in terms of multiple
performance criteria during their life cycle phases. Within this scope the phases
taken into account are manufacture, construction and occupancy. The ranges of
values for the pertinant criteria at each phase are tabulated below (Table 5).
Table 5
Ranges of Criteria Values at each Life
Cycle Phase
|
Phase |
Energy
(kW/m2) |
Waste
(kg/m2) |
Cost
(ECU/m2) |
Tolerance
(%) |
|
Manufacture |
2.7-4.6 |
1.6-3.2 |
94-215 |
1.5-4.2 |
|
Construction |
0.8-1.5 |
0.3-0.9 |
36-72 |
2.0-6.0 |
|
Occupancy |
0.2-1.3 |
0.1-0.5 |
7-15 |
5-15 |
While some of the criteria are in
accordance with each other, e.g. energy and waste, others are in conflict, e.g.
tolerance and cost. The utility functions of the criteria are deemed to be
linear and relative weights equal.
The instances of the consecutive stages are described below as they have
occurred.
Stage 1: The actual criterion values
of alternatives at each phase provide the input data for the subsequent
evaluation process. Then relative
values are obtained through standardization. Utility functions and if absolutely necessary, weights are
applied .
Stage 2: The statistical parameters
for these values, i.e. arithmetic mean, standard deviation and variaton
coefficient are calculated for each phase. They are then converted to relative
values to obtain an overall statistical performance indicator.
Stage 3: Table 6 presents the final
results that rank-order the alternatives that attain above-average utility
values at each phase and over the complete life cycle respectively. Individual
phases are also ranked.
Table 6
Ranked alternatives (A) and phases with above-average utility values
|
Rank |
Manufacture. |
Construction. |
Occupation |
Life
cycle |
Phase |
|||||
|
1 |
A8 |
9.52 |
A21 |
9.72 |
A8 |
9.54 |
A11 |
7.32 |
Manuf. |
5.35 |
|
2 |
A11 |
9.25 |
A8 |
8.74 |
A21 |
9.35 |
A6 |
6.38 |
Occup. |
5.18 |
|
3 |
A5 |
8.77 |
A17 |
7.45 |
A52 |
8.62 |
A21 |
6.26 |
Cons. |
4.72 |
|
4 |
A3 |
7.98 |
A11 |
6.78 |
A3 |
8.48 |
A8 |
6.53 |
|
|
|
5 |
A21 |
6.43 |
A3 |
5.36 |
A11 |
7.72 |
A3 |
5.27 |
|
|
|
6 |
A17 |
5.76 |
|
|
A8 |
6.28 |
A17 |
5.33 |
|
|
|
7 |
|
|
|
|
A22 |
5.37 |
|
|
|
|
|
8 |
|
|
|
|
A17 |
5.24 |
|
|
|
|
Conclusions
The proposed method explores design
alternatives and compares them in terms of relative performance for final
selection. The effect can be investigated of single or multiple design
variables on the overall performance of each alternative, while other
parameters remain constant. The actual variable values of the shortlisted alternatives can provide
guidance to designers for system development and contribute to an efficient
preparation of design specifications. Hence the method as a design tool enables
pre-defined performances of alternatives to be compared analytically.
In the context of life cycle analysis,
the method allows the performances of the following entities to be ascertained:
1. Alternatives at each phase or over the complete life cycle, 2. Phases of the
life cycle for the given set of alternatives.
The method is intended primarily for
the benefit of researchers as well as professionals involved in the design,
realization and management of buildings and their constituent parts for making
decisions between alternative solutions in their respective domains. Some
examples of application are provided below at various scales of design by the
pertaining discipline: Life-cycle
analysis of buildings or elements in terms of environmental impact, energy,
resource, cost and activity, Shape and size of building blocks and elements,
Floor shapes and areas of internal or external spaces, Modules of the
structural grid, Shape and size of structural members, Modules of façade
and floor elements, Combinations of layers within elements and their
thicknesses, Transparency ratio and aperture sizes in the external envelope,
Roof form and pitch, Composition of materials.
Appendix
(Alternative Generation)
This approach intends to provide the
amenity of alternative generation beside evaluation as an integral part of the
whole. For exploring the effect of different design configurations on
performance a combinatorial process of
alternative generation through exhaustive enumeration is here
implemented. Thus all plausible solutions are taken into consideration. Let I
be the number of design variables vi, each of which can take a different number
of discrete feasible values Ji
as decision options. These values are
combined to generate a total of (J1x...xJI)
alternatives. Obviously, the number of design alternatives is directly
proportional to the number of design variables and also of their prospective values.
Only the incoherent variables , i.e. those requiring a compromise, are
selected. The remainder are taken as constants to which the appropriate extreme
values are assigned. The number of viable alternatives can be further reduced
by elimination of those containing incompatible values of any two or more
variables. An interaction matrix allows paired compatibility to be examined,
based on analytical or heuristic knowledge as illustrated in Table 7, where the
plus and minus signs denote the compatible and incompatible value pairs respectively.
The first subscript denotes the variable type and the second the discrete
values, i.e. the instances that may be in different numbers for each variable.
Table 7
Compatibility Matrix for Values of Any
Two Variables (v)
|
v2, 1 |
+ |
|
|
|
|
v2, j |
- |
+ |
|
|
|
vi, 1 |
+ |
+ |
- |
|
|
vi, j |
+ |
+ |
+ |
+ |
|
|
v1,
1 |
v1, j |
vi-1,
1 |
vi-1,
j |
The procedure described
above is iterated for each design parameter in the case of systems with
multiple physical components. A combination is possible for each parameter, the
main ones of which, as examplified below by building elements, are:
1. Components included (e.g. external
finish, thermal insulation, damp-proof membrane, etc.),
2. Order of Components (e.g. thermal
insulation outside or inside damp-proof membrane),
3. Alternatives of Components (e.g.
for external finish: render, sheet, panel, etc.)
The
total number of design alternatives is obtained by multipying the combinations
of all parameters.
References
1. H.
MÜLLER, Lehrbuch der
Hochbaukonstruktionen: Methodik des Konstruierens, Cziesielski, E., Ed.,
Teubner, Stuttgart, 1990, pp.9-24.
2. R.P.
REDDY, F. MISTREE, Modeling Uncertainty in Selection Using Exact Interval
Arithmetic, Design Theory and
Methodology, The American Society of Mechanical Engineers, New York,
Vol.42, 1992, pp.193-201.
3. G.
IYENGAR, C.L. LEE, S. KOTA, Towards an Objective Evaluation of Alternative
Designs, Design Theory and Methodology,
American Society of Mechanical Engineers, New York, Vol.42, 1992, pp.19-25.
4. W.R.
SIMS, F.D. BECKER, Matching Building Performance to Organizational Needs, Performance of Buildings and Serviceability
of Facilities, ASTM STP 1029, Davis, G. and Francis, T., Eds., American
Society for Testing And Materials, Philadelphia, 1990, pp.289-310.
5. M.
BOUBEKRI, Z. YIN, R. GUY, A Neural Network Solution to an Architectural Design
Problem: Design of a Light Shelf, Architectural
Science Review, Vol.40, no.1, 1997, pp.17-21.
6. N.
D'CRUZ, A. RADFORD, A Multicriteria Model for Building Performance and Design, Building and Environment, Vol.22, No.3,
Pergamon Press, London, 1987, pp.167-179.
7. N.
CROSS, Engineering Design Methods,
John Wiley & Sons,
8. D.G.
ULLMAN, The Mechanical Design Process,
International Edition, McGraw-Hill Inc.,
9. R.
COYNE, Logic Models of Design, Pitman
Pub.,
10. Z. HATUSH,
M. SKITMORE, Contractor Selection Using Multicriteria Utility Theory: An
Additive Model, Building and Environment,
Elsevier Science Ltd., Vol.33, No.2-3,