Symbolic Algebra in Control Engineering
Symbolic Algebra (or so called Computer Algebra) can be extensively used in many areas of control engineering. This document illustrates just a few of these areas and is prepared as an aid to the technical paper [1]. As the symbolic algebra programming environment Mathematica is used in the following.
It is actually possible to view the main advantages of the use of symbolic algebra in two categories.
1. Exact Calculations
2. Manipulation of Symbols
1. Exact Calculations
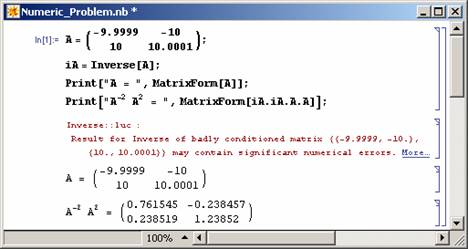
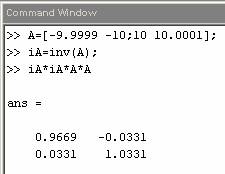
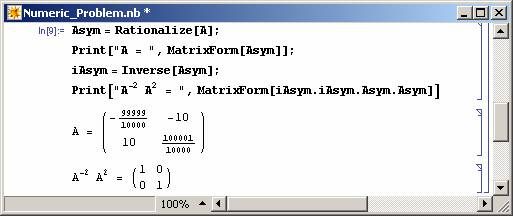
Computer algebra allows us to do exact calculations. This is particularly useful in numerically error prone procedures. Consider the numerical problem illustrated in Figure 1. The problem can be overcome by using rational (exact) numbers as shown in Figure 2.
|
|
|
|
(a) |
(b) |
|
Figure 1: Example on errors that may result after numerical calculations (a: Mathematica, b: Matlab). |
|
|
Figure 2: Example on symbolic calculations (Mathematica Code). |
Click on the picture to download the Mathematica file.
2. Manipulation of Symbols
Computer algebra languages can handle symbolic expressions. This is useful in many areas of control engineering, where complex formulations are ubiquious.
2.1 Block Diagram Reduction
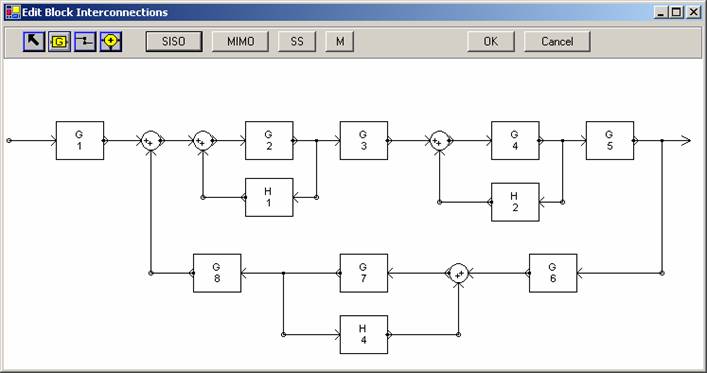
It is possible to calculate the transfer functions (or state-space representations) of the closed-loop system from those of subsystems by the help of symbolic manipulations as illustrated in [2]. The block diagram reduction toolbox allows users to draw the block diagram of a system using .NET technology and then calculate the closed-loop system transfer functions both for SISO and MIMO case. The toolbox can also find the state space representation of the closed-loop system.
|
|
|
Figure 3: A block diagram drawn in Block Diagram Reduction Toolbox |
Take the block diagram given in Figure 3 as an example. The toolbox can calculate the closed-loop system transfer function (by pressing the SISO button) as shown in Figure 4.
|
|
|
Figure 4: Calculation of the closed-loop system transfer function. |
Note that it is possible to use explicit expressions for the transfer functions of the subsystems (see Figure 5 as an example).
|
|
|
Figure 5: Calculating the closed-loop system transfer function explicitly. |
It is also possible to obtain the closed-loop system transfer function in terms of numerators and denominators of the subsystems (See Figure 6). Note that this way the closed-loop system characteristic polynomial, which purely depends on system topolgy, can be obtained. This is considered to be one of the unsolved problems in Control Theory [3].
|
|
|
Figure 6: Calculation of the closed-loop system characteristic polynomial in terms of numerators and denominators of transfer functions of the subsystems. |
2.2 Calculation of Stabilizing Gains
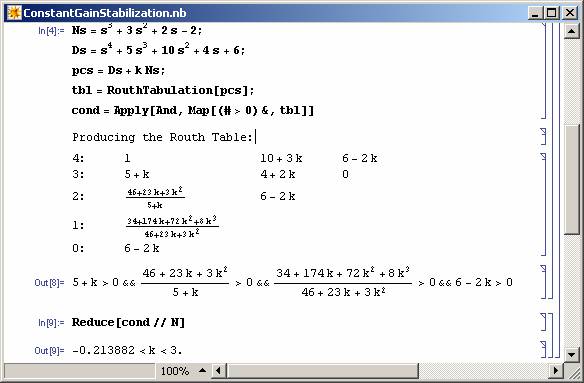
Calculation of stabilizing gains has taken a lot of attention recently (see e.g. [4]). Simple and direct use of symbolic algebra can help us solve this problem directly (see Figure 7). Note that the Routh Table of the closed-loop system is produced symbolically to achieve the desired answer here. To download the RouthTabulation procedure click here.
|
Figure 7: Solving a constant feedback stabilization problem using Mathematica. |
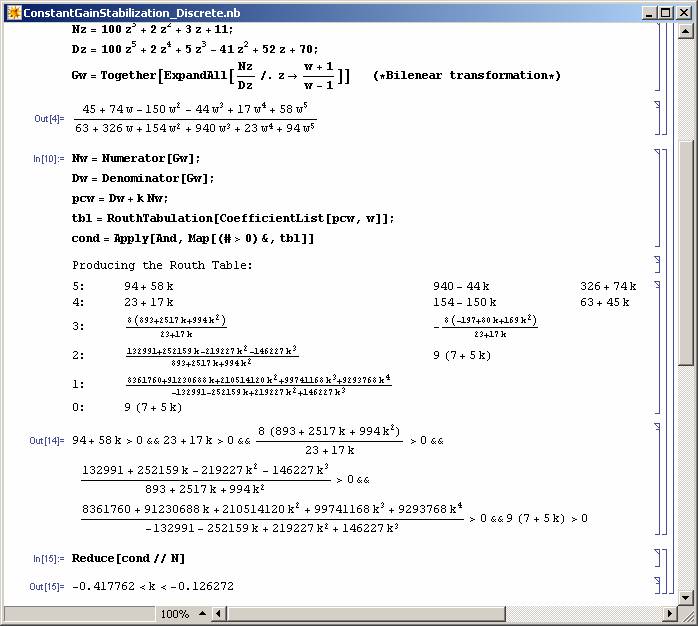
Note that it is also possible to find stabilizing intervals for discrete-time systems (see Figure 8).
|
Figure 8: Finding stabilizing gain intervals for a discrete time system. |
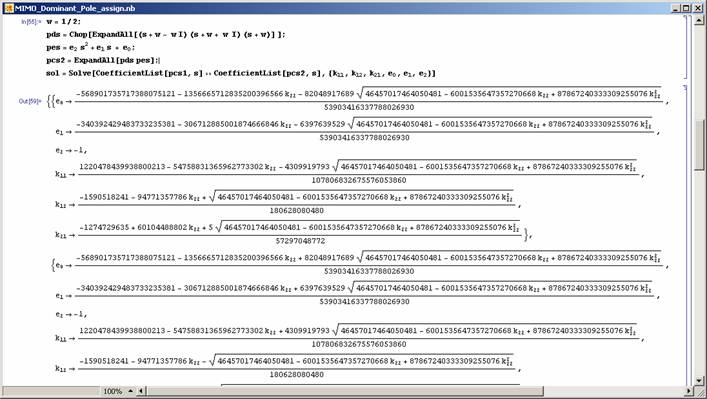
2.3 Dominant Pole Assignment
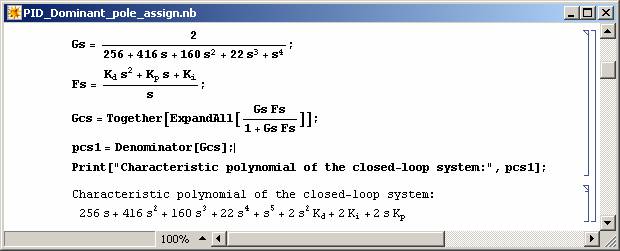
Computer algebra can be used to solve the dominant pole assignment problem directly, without the need for applying any algebraic methods such as the solution of polynomial Diophontine equations. Take the example given in Figure 9 and 10, where the dominant poles of the closed-loop system is required to be assigned at -1/2 + 1/2 j and -1/2 - 1/2 j using a PID controller.
|
Figure 9: Finding the closed-loop system characteristic polynomial. |
|
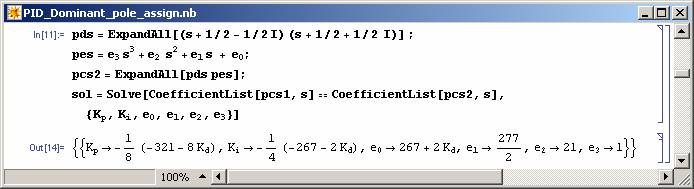
Figure 10: Solving the dominant pole assignment problem for Example 3.2. |
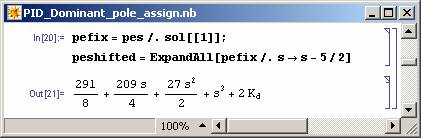
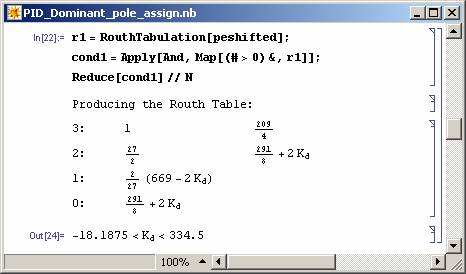
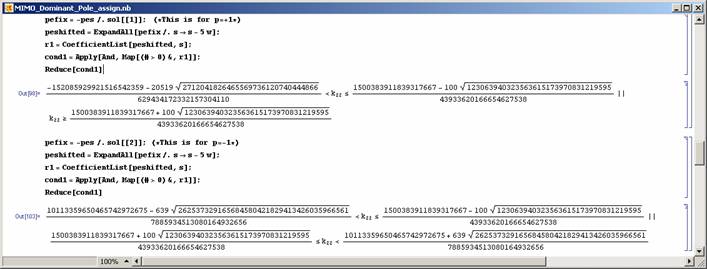
Note that a parametric solution is obtained for the problem and all the values of Kd will result in two of the closed-loop system poles to be at required places. For these poles to be dominant the rest of the closed-loop system poles (the roots of pe(s)) should be on the left of -5/2 line. This can be achieved as shown in Figure 11 and 12.
|
Figure 11: Finding pe(s-5/2). |
|
Figure 12: Restricting non-dominant poles. |
Now if Kd is selected between -18.1875 and 334.5 in the above solution then the dominant pole assignment is achieved. It is also possible to restrict the zeros of the controller to be left of -5/2 line (see Figure 13).
|
Figure 13: Restricting PID zeros. |
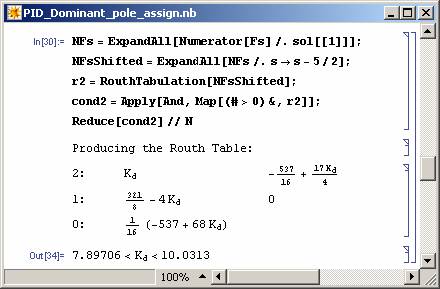
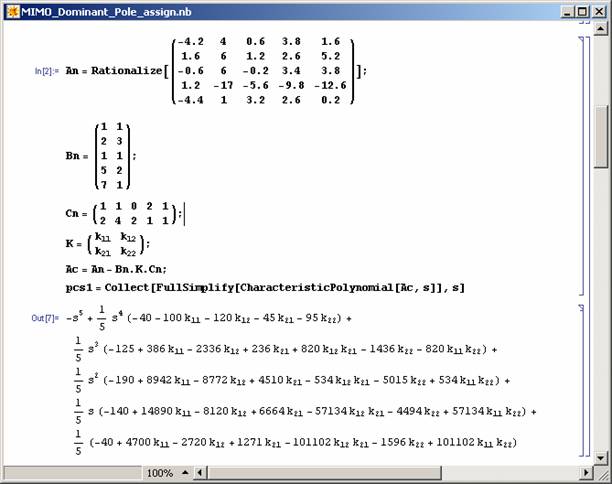
It should be noted that the above procedure can be applied to other kinds of controllers and for simple MIMO systems (see Figure 14-16).
|
Figure 14: Finding the closed-loop system characteristic polynomial. |
|
Figure 15: Solution of the dominant pole assignment problem . |
|
Figure 16: Restricting non-dominant poles. |
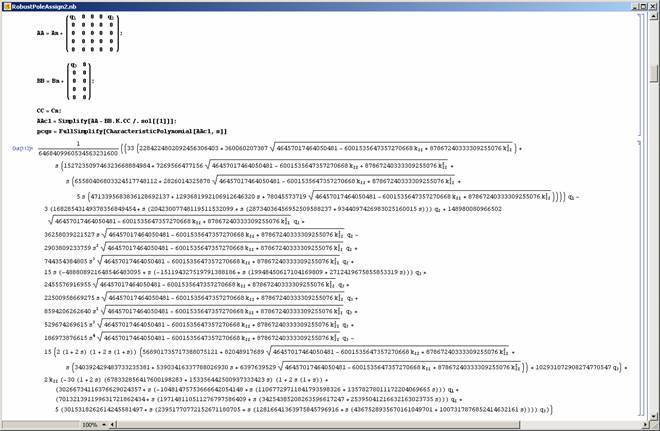
2.4 Control of Systems with Parameter Uncertainty
In many cases symbolic algebra can be used to obtain algebraic expressions which are to be used in further optimizations. Robust pole assignment for parametric uncertain systems is one such area (see [5]). Here, the closed-loop system characteristic polynomial is obtained in the most general form in terms of free controller parameters and uncertain parameters (as in Figure 17) before engaging an optimization algorithm.
|
|
|
Figure 17: Calculation of the pc(s,q,k). |
References
[1] M. T. Söylemez and İ. Üstoğlu (2006), "Designing Control Systems using Exact and Symbolic Manipulations of Formulae", submitted to Int. J. of Control.
[2] M T Söylemez and İ. Üstoğlu (2004,6), "Block Diagram Reduction Using Symbolic Algebra", IEEE Mediterranean Conference on Control and Automation (MED'04), Kusadası, Turkey.
[3] A. D. Lewis (2004), What is the characteristic polynomial of a signal flow graph?, in Unsolved Problems in Mathematical Systems and Control Theory, V. D. Blondel and A. Megretski, Ed., Princeton University Press, ISBN:0-691-11748-9, available at http://www.pupress.princeton.edu/math/blondel/.
[4] N. Munro, M. T. Söylemez and H. Baki (1999), Computation of D-Stabilizing low-order compensators, Control System Centre Report 882, UMIST, Manchester, UK.
[5] N. Munro and M. T. Söylemez (1996), The use of symbolic algebra in pole assignment for uncertain systems, in UKACC Int. Conf. on Control96, Exeter, UK, September, pp 1332 1337.