Veri Biliminde İstatistik ve Makina Öğrenmesi Metodları
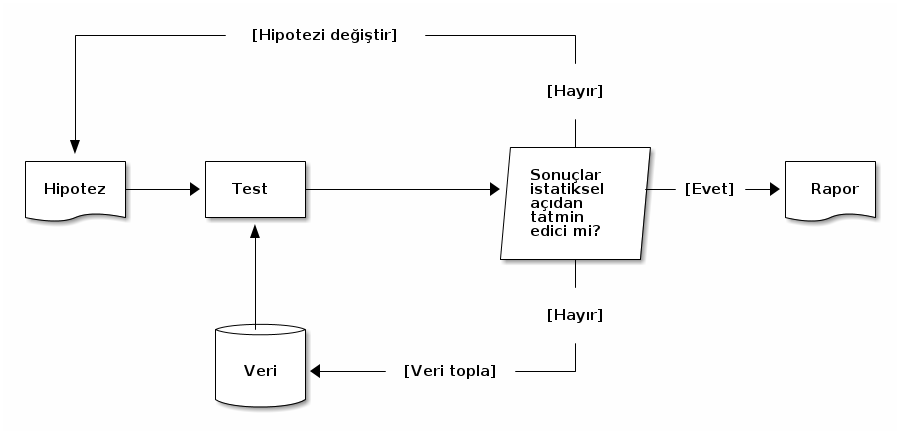
1 Benzer mi, farklı mı?
1.1 t-testi
Varsayalım ki elimizde iki sunucunun kendilerine aynı anda verilen bir isteği teslim etme sürelerini gösteren dizi sayı dizisi olsun.
veri <- data.frame(sunucuA = c(0.17, 0.24, 0.11, 0.28, 0.21, 0.19),
sunucuB = c(0.26, 0.21, 0.20, 0.12, 0.13, 0.13))
veri
sunucuA sunucuB 1 0.17 0.26 2 0.24 0.21 3 0.11 0.20 4 0.28 0.12 5 0.21 0.13 6 0.19 0.13
Sorumuz bu iki sunucunun isteklere cevap verme süreleri arasında istatiksel olarak bir fark gözleyebilip gözleyemeyeceğimiz olsun. İlk bakışta sunucuların ortalama cevap verme sürelerinin farklı olduğunu görebiliyoruz.
mean(veri$sunucuA) mean(veri$sunucuB)
[1] 0.2 [1] 0.175
Ancak veri kümemizdeki eleman sayısının fazla olmadığına dikkat edin. Bu da arada bir farkın olmaduğunu istatistiksel bir kesinlikle söyleyebilmemize engel olabilir. Bunu öğrenmek için Student'in t-testini uygulayacağız.
t.test(veri$sunucuA, veri$sunucuB)
Welch Two Sample t-test
data: veri$sunucuA and veri$sunucuB
t = 0.74981, df = 9.9901, p-value = 0.4707
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.04929984 0.09929984
sample estimates:
mean of x mean of y
0.200 0.175
Bu testin sonucunda dikkat etmemiz gereken değer confidence interval
değeridir. t-testin sonucuna göre aradaki fark %95 olasılıkla -0.05
ile 0.10 arasındadır. Demek ki sunucunun cevap verme süreleri
arasındaki farkın sıfırdan farklı olduğunu göremiyoruz.
Dikkat edileceği üzre testin uygulanabilmesi için veri noktalarının ikişer ikişer gelmesi gerekiyor. Eğer veri noktaları çiftler şeklinde gelmediyse o zaman başka metodlar uygulamamız gerekir.
1.2 Kolmogorov-Simirnov testi
Varsayalım ki elimizde aynı dersi alan iki şube öğrenci olsun ve bu öğrenciler aynı soruları çözdükleri ilk sınavlarından 10 üzerinden şu notları almış olsunlar.
subeA <- c(2,9,8,6,7,3,5,2,8,5,9,7,9,4,6,8) subeB <- c(6,1,4,2,4,3,6,2,3)
Bu iki grup öğrenci arasında bir fark olup olmadığını öğrenmek istiyoruz.
mean(subeA) mean(subeB)
[1] 6.125 [1] 3.444444
Bu durumda veri noktaları çiftler şeklide gruplanamıyorlar. O yüzden t-testini kullanamıyoruz. Yukarıda t-testinde kullandığımız örneği düşünürsek ortalamalar arasında görünen farktan istatistiksel olarak emin olup olamayacağımızı bilmiyoruz. Bu durumda bu iki grup arasında fark olup olmadığını bulmak için Kolmogorov-Smirnov testi'ni kullanacağız.
ks.test(subeA, subeB)
Two-sample Kolmogorov-Smirnov test
data: subeA and subeB
D = 0.52778, p-value = 0.0808
alternative hypothesis: two-sided
Warning message:
In ks.test(subeA, subeB) : cannot compute exact p-value with ties
Burada bakmanız gereken istatistik D = 0.5. Bu değer 0.0 ve 1.0
arasında gelir. Demek ki onemli bir fark görüyoruz. Sonra bakmamız
gereken değer ise p-value = 0.08. Çıkan sonuca göre %92 olasılıkla
bu iki grubun birbirınden farklı olduğunu söyleyebiliriz.
1.3 Torbalama (Bootstrapping)
Torbalama tekniği eğer elimizde yeterince veri noktası yoksa uygulayabileceğimiz bir teknik. Ancak hesaplama ağırlığı fazla olduğu için elimızdeki veri kümesi çok büyük ise kaçınılması gerekir.
Basitçe anlatırsak:
- Elimizdeki veri kümesinden gelişi güzel noktalar çekip, kaydedip geri koyalım.
- Bu torba üzerinde gözlemlemek istediğimiz istatistiği (ortalama, varyasyon vb.) hesaplayalım. Bunu bir yere kaydedelim.
- Adım 1 ve 2'yi gerekli olduğu kadar tekrarlayalım. Adım 2'den yeterince veri noktası gelince duralım.
Merkezi Limit Teoremi'ne göre 2. adımda hesapladığımız değerler Gaussian dağılıma göre dağılmış olan bir raslantısal bir değişkendir.
Aşağıdaki kodda tanımladığımız fonksiyon, yukarıda subeA olarak
tanımladığımız veri kümesinden rastgele 100 tane nokta çeker ve
bunların ortalamasını hesaplar. Bunu 1000 kere tekrarlayıp torba
adlı listenin içine yazıyoruz. Bu değerleri sıralıyoruz.
deney <- function(x) {
mean( sample( subeA, 100, replace=TRUE ) )
}
torba <- sort( sapply(1:1000, deney))
c( torba[25], torba[975] )
[1] 5.66 6.58
Bu değerlerin 25. ve 975.ne bakarsak %95 olasılıkla ortalamaların hangi aralıkta olduğunu görüyoruz.
Bunu yapmanın başka bir yolu da t.test fonksiyonunu dogrudan
subeA'ya uygulamaktır.
t.test(subeA)
One Sample t-test
data: subeA
t = 10.13, df = 15, p-value = 4.218e-08
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
4.836178 7.413822
sample estimates:
mean of x
6.125
Değerlerin aynı olmadığına dikkat edin. Genelde torbalama tekniği daha iyimser sonuçlar (daha dar aralıklar) verir.
2 Aralarında ilişki var mı yok mu?
2.1 χ2-testi
R deney yapmak icin hazır veri kümeleri ile beraber gelir. Bunlardan
biri de HairEyeColor veri kümesidir. Bu küme 3 boyutlu bir matris
olup 1974'te Profesör Snee'nin Delaware Üniversitesindeki
öğrencilerden topladığı bir kümedir.
veri <- HairEyeColor veri
, , Sex = Male
Eye
Hair Brown Blue Hazel Green
Black 32 11 10 3
Brown 53 50 25 15
Red 10 10 7 7
Blond 3 30 5 8
, , Sex = Female
Eye
Hair Brown Blue Hazel Green
Black 36 9 5 2
Brown 66 34 29 14
Red 16 7 7 7
Blond 4 64 5 8
Bu kümeden erkek ve kadın farkını (3. boyut) kaldıralım:
yeni <- HairEyeColor[,,1] + HairEyeColor[,,2] yeni
Eye
Hair Brown Blue Hazel Green
Black 68 20 15 5
Brown 119 84 54 29
Red 26 17 14 14
Blond 7 94 10 16
Sorumuz saç ve göz renkleri arasında istatistiksel kesinlikle görünen bir ilişki olup olmadığı.
chisq.test(yeni)
Pearson's Chi-squared test
data: yeni
X-squared = 138.29, df = 9, p-value < 2.2e-16
Görüldüğü üzre, p-value oldukça ufak. Bu da elimizdeki verinin bu
şekilde gelen bütün veriler arasında görünme olasılığının düşük
olduğunu söylüyor. X-squared İstatistiğinin büyük olması ise bu iki
değişkenin arasındaki ilişkinin çok kuvvetli olduğunu gösterir. Öte
yandan cinsiyet ve saç rengi arasındaki ilişkiyi test etmek istersek:
dene <- HairEyeColor[,1,] + HairEyeColor[,2,] dene chisq.test(dene)
Sex
Hair Male Female
Black 43 45
Brown 103 100
Red 20 23
Blond 33 68
Pearson's Chi-squared test
data: dene
X-squared = 9.3483, df = 3, p-value = 0.025
aralarında bir ilişki olduğunu ancak bu ilişkinin daha zayıf olduğunu görebiliyoruz. Şimdi de göz rengi ve cinsiyet ilişkisine bakalım:
dene <- HairEyeColor[1,,] + HairEyeColor[2,,] dene chisq.test(dene)
Sex
Eye Male Female
Brown 85 102
Blue 61 43
Hazel 35 34
Green 18 16
Pearson's Chi-squared test
data: dene
X-squared = 4.7529, df = 3, p-value = 0.1908
Aralarında istatiksel kesinlikle iddia edebileceğimiz bir ilişki göremiyoruz.
2.1.1 Dikkat edilmesi gereken noktalar
χ2 Testi tablo haline getirebileceğimiz ayrık kategorik değişkenler için kullanılmalıdır. Örneğin yukarıda kullandığımız veri kümesi ya da aşagıdaki veri kümesi gibi.
head(data.frame(Titanic))
Class Sex Age Survived Freq 1 1st Male Child No 0 2 2nd Male Child No 0 3 3rd Male Child No 35 4 Crew Male Child No 0 5 1st Female Child No 0 6 2nd Female Child No 0
2.2 Korelasyon
Eğer elimizdeki veri nümerik veri ise o zaman χ2-testini kullanamayız. Onun yerine iki veri kümesi arasında lineer bir ilişki olup olmadığını test edebiliriz.
Bır sonraki örnek için iris veri kümesini kullanacağız.
head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa
İlk olarak nümerik kolonlar arasında ne tür ilişkiler var ona bakalım:
cor( iris[,1:4] )
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000
Diagonalin 1.0 çıkması beklenir bir şeydir. Sonuçta her kolon kendisine sıkı bir şekilde bağlıdır. Bunun ötesinde görüyoruz ki Sepal uzunluk ve Petal uzunluk arasında pozitif ve kuvvetli bir ilişki var: biri arttığında diğeride onunla beraber artmaktadır. Bunun tersine Petal uzunluk arttığında Sepal genişlik ise düşmektedir. Sepal genişlik ve uzunluk arasında da buna benzer bir ilişki bulunmakta ancak bu ilişki Petal uzunluk ve Sepal genişlik arasındaki ilişkiden daha zayıftır.
3 Regresyon modelleri
3.1 Numerik regresyon
Yukarıdaki iris veri kümesi örneğinde kolonlar arasındaki
korelasyonu bulmuştuk. Şimdi de bunu kullanarak nasıl istatistiksel
bir model geliştirebileceğimize ve bu modelden nasıl tahminde
bulunabileceğimizi görelim.
Varsayalım ki Petal genişliği Sepal genişlik ve uzunluk cinsinden yazmak istiyoruz. Önce veri kümemizi eğitim (%75) ve dogrulama (%25) verisi olarak iki parçaya bölelim.
N <- nrow(iris) egit <- sample(1:N, floor(0.75*N), replace=FALSE) dogrula <- -egit
Şimdi de lineer regresyon modelimizi kuralım:
model <- glm ( Petal.Length ~ Sepal.Length + Sepal.Width, data = iris, subset = egit)
Bu modeli kullanarak dogrula veri kümesi üzerinde Petal uzunlukları
tahmin edelim.
tahmin <- predict(model, iris[dogrula,])
Yanlız hatırlayalım ki Petal uzunlukların gerçek değerlerini biliyoruz. Ortalama (göreli) hatayı ölçelim:
a <- min(iris$Petal.Length[dogrula]) b <- max(iris$Petal.Length[dogrula]) err <- mean( abs(tahmin - iris$Petal.Length[dogrula]) ) err/(b-a)
[1] 0.09995596
Ortalama hatanın düşük olması (yaklaşık %10) göstermektedir ki Petal uzunluğu, Sepal uzunluk ve genişlik verilerinden istatistiksel olarak tatmin edici bir biçimde çıkartmamız mümkün görünuyor.
3.2 Multinomyel regresyon
Eğer bağımlı değişkenimiz ayrık değerli bir değişken ise o zaman
multinomyel regresyon metodunu kullanabiliriz. Bu kısımda yukarıda
kullandığımız iris veri kümesini yeniden kullanacağız.
Yine elimizdeki veriyi iki parçaya bölelim:
N <- nrow(iris) egit <- sample(1:N, floor(0.75*N), replace=FALSE) dogrula <- -egit
Multinomyel regresyon için nnet kütüphanesine ihtiyacımız var.
library(nnet)
Modelimizi kuralım:
model <- multinom( Species ~ . , data=iris, subset=egit) sonuc <- predict(model, iris[dogrula,]) tablo <- table(hesaplanan = sonuc, gercek = iris$Species[dogrula]) tablo
# weights: 18 (10 variable)
initial value 123.044576
iter 10 value 12.245445
iter 20 value 2.647394
iter 30 value 1.386576
iter 40 value 1.137896
iter 50 value 0.828985
iter 60 value 0.730253
iter 70 value 0.711031
iter 80 value 0.666706
iter 90 value 0.531543
iter 100 value 0.444413
final value 0.444413
stopped after 100 iterations
gercek
hesaplanan setosa versicolor virginica
setosa 13 0 0
versicolor 0 13 2
virginica 0 0 10
Başarı oranımızı hesaplayalım:
(tablo[1,1]+tablo[2,2]+tablo[3,3])/sum(tablo)
[1] 0.9473684
3.3 Log-lineer modeller
Log-lineer modeller ayrık değerli veri kümelerinde veri değerlerinin sıklıkları arasındaki ilişkileri incelemek için kullanılır.
veri <- data.frame(Titanic) head(veri)
Class Sex Age Survived Freq 1 1st Male Child No 0 2 2nd Male Child No 0 3 3rd Male Child No 35 4 Crew Male Child No 0 5 1st Female Child No 0 6 2nd Female Child No 0
Tahmin etmek istediğimiz değişken sıklık değişkeni (Freq) olduğu için modelimizi aşağıdaki gibi kuracağız.
model <- glm( Freq ~ . , data = veri, family=poisson) exp(model$coefficients)
(Intercept) Class2nd Class3rd ClassCrew SexFemale AgeAdult 8.5690577 0.8769231 2.1723077 2.7230769 0.2715194 19.1926605 SurvivedYes 0.4771812
Yukarıda hesapladığımız sayılar bir referans değerine göre olasılık oranlarıdır.
- Bir çocuğun kurtulmuş olması olasılığı bir yetişkinin kurtulmuş olması olasılığının yaklaşık 19 katıdır.
- Titanik'in 1. Sınıf kabinde kalan bir yolcunun kurtulmuş olması olasılığı 3. sınıf kabinde kalan bır yolcunun kurtulmuş olması olasılığının yaklaşık 2 katıdır.
Referans değerlerini aşağıdaki gibi değiştirebiliriz:
veri <- within(veri, Class <- relevel(Class, ref = "2nd")) veri <- within(veri, Sex <- relevel(Sex, ref = "Female")) model <- glm( Freq ~ . , data = veri, family=poisson) exp(model$coefficients)
(Intercept) Class1st Class3rd ClassCrew SexMale AgeAdult 2.0403062 1.1403509 2.4771930 3.1052632 3.6829787 19.1926605 SurvivedYes 0.4771812
Bu yeni oranlardan
- bir kadının kurtulmuş olması olasılığı bir erkeğin kurtulmuş olması olasılığının yaklaşık 3.7 katı
- ikinci sınıf kabinde yolculuk eden bir yolcunun kurtulmuş olması bir gemi çalışanının kurtulmuş olması olasılığının yaklaşık 3 katı
olduğunu görüyoruz.
4 Öbekleme ve sınıflandırma
Öbekleme ve sınıflandırma algoritmaları eldeki veri kümesinin noktalarının etiketlenerek parçalanması için kullanılır.
4.1 k-ortalamalar
Bu algoritmada veri kümesini kaç parçaya böleceğimiz baştan bir k sayısı verilerek belirtilir. Veri kümemizin noktalarının bir vektör uzayı içine oturtulmuş olması gerekir: veri setinin bütün kolonları nümerik olmalıdır. Algoritmayı kısaca şöyle anlatabiliriz:
- Veri kümesi içinden rastgele k nokta y1 ,…, yk seçelim, ve bunları 1'den k'ya kadar sayılarla işaretleyelim.
- Veri kümesindeki her x noktasının yi'lere olan uzaklıklarını ölçelim ve x'in etiketini x'e en yakın noktanın etiketi olarak belirleyelim.
- Her etiket j için, j etiketine sahip olan bütün noktaların merkezlerini mj hesaplayalım.
- Eğer bütün j'ler için mj'ler ve yj'ler arasındaki uzaklık başta belirlediğimiz bir eşik değerinin altındaysa o zaman algoritmayı bitireceğiz.
- Eğer algoritma 4. adımda bitirilmediyse o zaman 2. adıma geri dönelim.
Bu kısımda veri kümemizi dogrudan web'den indireceğiz. Kullanacağımız veri UCI'ın şarap veri kümesi olacak.
sarap <- read.csv("https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data",
header=FALSE)
head(sarap)
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 1 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065 2 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050 3 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185 4 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480 5 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735 6 1 14.20 1.76 2.45 15.2 112 3.27 3.39 0.34 1.97 6.75 1.05 2.85 1450
Veri kümesi şarapları 3 kümeye bölmüş şekilde geliyor. İlk kolon bu etiketi gösteriyor. Öncelikle bütün kolonları normalize edelim.
veri <- c()
for(i in 2:14) {
veri <- cbind(veri, (sarap[,i] - mean(sarap[,i]))/var(sarap[,i]))
}
veri <- data.frame(veri)
sonuc <- kmeans(veri,3)
tablo <- table(hesaplanmis = sonuc$cluster, gercek = sarap[,1])
tablo
gercek
hesaplanmis 1 2 3
1 12 33 0
2 45 19 10
3 2 19 38
Etiketler başlangıçta gelişi güzel seçıldiği için, başta verilen sınıflarla uyum göstermesini bekleyemeyiz. Dolayısıyla başarıyı diagonal üzerinde ölçemeyecegiz. Tablodaki değerler arasındaki ilişkinin kuvvetini ölçmek için χ2 testini kullanacağız.
chisq.test(tablo)
Pearson's Chi-squared test
data: tablo
X-squared = 98.429, df = 4, p-value < 2.2e-16
4.2 k-en yakın komşular
Bu algoritma da bir önceki metod gibi elimizdeki veri kümesini kendi içinde benzeyen parçalara bölmek için kullanılır. Bu metodu kullanabilmemiz için elimizdeki veri kümesinin eğitim veri alt kümesinde veri noktalarının etiketlerini bilmemiz gerekiyor. Elimizde etiketlenmesi gereken bir nokta olsun.
- Bu noktanın etiketleri bilinen kümedeki elemanlara uzaklıkları hesaplanır.
- Bu noktaya en yakın k tane noktaya bakılır.
- Bu noktaların etiketleri sayılır ve en çok gorülen etiket elimizde etiketi bilinmeyen noktaya etiket olarak atanır.
Bu örnek için iris veri kümesini kullacağız.
library(class) N <- nrow(iris) egit <- sample(1:N, 0.75*N, replace=FALSE) dogrula <- -egit tahmin <- knn(iris[egit,1:4], iris[dogrula,1:4], iris$Species[egit], k = 4, prob = FALSE) tablo <- table(tahmin, gercek = iris$Species[dogrula]) tablo
gercek
tahmin setosa versicolor virginica
setosa 11 0 0
versicolor 0 14 0
virginica 0 1 12
Şimdi başarı oranımızı hesaplayalım:
(tablo[1,1]+tablo[2,2]+tablo[3,3])/sum(tablo)
[1] 0.9736842
4.3 Basit Bayes sınıflandırma
4.4 Karar ağaçları
Karar ağaçları elinizdeki ayrık bağımlı bir değişkeni tahmin etmek için kullanılır. Algoritma bunu yapmak için veri kolonlarını bağımlı değişkende en büyük değişikliği yapacak biçimde bölmeye çalışır.
Bu kısımdaki örnek için yukarıda kullandığımız şarap veri kümesini
kullanacağız. Karar ağaçlarını kullanmak için party kütüphanesi
kullanacağız. Model oluşturma kodu daha önce kullandığımız model
kodlarına çok benzediği için çok bir açıklama yapmayacağız.
library(party) N <- nrow(sarap) egit <- sample(1:N, 0.7*N, replace=FALSE) dogrula <- -egit model <- ctree(V1 ~ . , data = sarap, subset = egit) plot(model, type="simple")
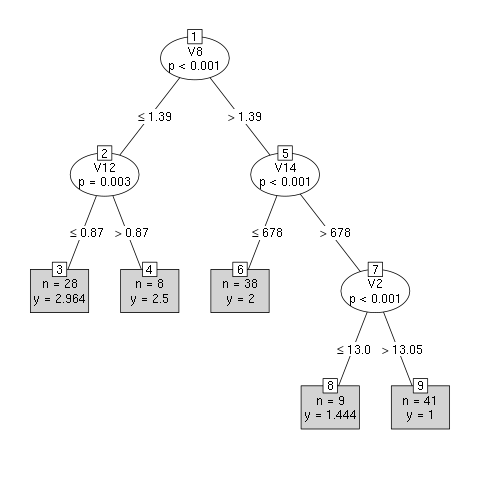
Modelimizi test edelim:
tahmin <- predict(model, sarap[dogrula,]) tablo <- table(hesaplanan = round(tahmin), gercek = sarap$V1[dogrula]) tablo
gercek
hesaplanan 1 2 3
1 13 4 0
2 0 20 1
3 0 0 16
Başarı oranımızı da hesaplayalım:
(tablo[1,1]+tablo[2,2]+tablo[3,3])/sum(tablo)
[1] 0.9074074
4.5 Rastlantısal ormanlar (random forests)
Raslantısal ormanlar birden çok karar ağacı birleştirilerek kurulan
bir istatitik metodudur. Ancak neyse ki R ya da python gibi bir
dil kullanıyorsanız, dil içindeki kütüphaneler bu metodun kullanımını
kolaylaştırmaktadır.
Bu kısımdaki örnek için Amerikan Parlamentosu oylama veri kümesini kullanacagız.
library(randomForest)
oylar <- read.csv("https://archive.ics.uci.edu/ml/machine-learning-databases/voting-records/house-votes-84.data",
header=FALSE)
N <- nrow(oylar)
egit <- sample(1:N, 0.75*N, replace=FALSE)
dogrula <- -egit
model <- randomForest(V1 ~ . , data = oylar, subset = egit)
tablo <- table(hesaplanan = predict(model, oylar[dogrula,]), gercek = oylar$V1[dogrula])
tablo
(tablo[1,1]+tablo[2,2])/sum(tablo)
gercek
hesaplanan democrat republican
democrat 68 1
republican 2 38
[1] 0.9724771
Bu sonuçları karar ağacı metodundan elde edeceğimiz sonuçla karşılaştıralım:
model <- ctree(V1 ~ . , data = oylar, subset = egit) tablo <- table(hesaplanan = predict(model, oylar[dogrula,]), gercek = oylar$V1[dogrula]) tablo (tablo[1,1]+tablo[2,2])/sum(tablo)
gercek
hesaplanan democrat republican
democrat 61 0
republican 9 39
[1] 0.9174312
Aralarında çok büyük bir fark göremiyoruz. Bunun temel nedeni bağımlı değişkenin sadece iki farklı değer alması, çok farklı sayıda değer almamasıdır. Eğer bağımlı değişken az sayıda değer alıyorsa o zaman ya bir monomyel regresyon ya da karar ağacı kullanılması daha uygun olacaktır.
4.6 SVM
SVM teknik olarak yüksek boyuntlu bir vektör uzayı içine gömülmüş bir
veri kümesini sadece iki farklı değer alan bagımlı bir değişkene göre
ikiye bölmek için geliştirilmiştir. Ancak birden fazla SVM modeli
yanyana kullanılarak sonlu sayıda farklı değer alan bagımlı bir
değişkene göre de eldeki veri parçalanabilir. R ve pthon gibi
dillerin kullandıkları SVM kodu bu şekilde çalışacak şekilde
yazılmıştır.
Şimdi bu metodu sarap veri kümesi üzerinde uygulayalım:
N <- nrow(sarap) egit <- sample(1:N, 0.75*N) dogrula <- -egit model <- svm( V1 ~ . , scale = TRUE, data = sarap, subset = egit) sonuc <- round(predict(model, sarap[dogrula,])) tablo <- table(hesaplanan = sonuc, gercek = sarap$V1[dogrula]) tablo (tablo[1,1]+tablo[2,2]+tablo[3,3])/sum(tablo)
gercek
hesaplanan 1 2 3
1 17 0 0
2 1 17 1
3 0 0 9
[1] 0.9555556